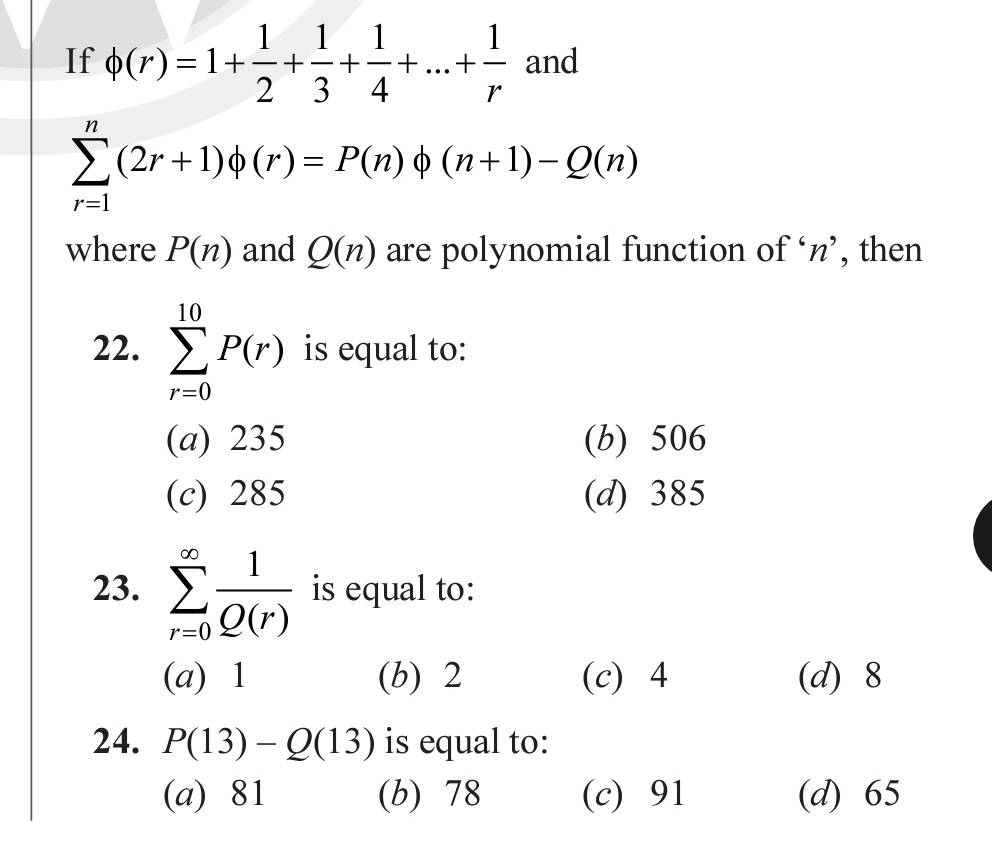
If \( \phi(r)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots+\frac{1}{r} \) and \( \sum_{r=1}^{n}(2 r+1) \phi(r)=P(n) \phi(n+1)-Q(n) \)
where \( P(n) \) and \( Q(n) \) are polynomial function of ' \( n \) ', then
22. \( \sum_{r=0}^{10} P(r) \) is equal to:
(a) 235
(b) 506
(c) 285
(d) 385
23. \( \sum_{r=0}^{\infty} \frac{1}{Q(r)} \) is equal to:
(a) 1
(b) 2
(c) 4
(d) 8
24. \( P(13)-Q(13) \) is equal to:
(a) 81
(b) 78
(c) 91
(d) 65