We have
(D2 – 2D + 3)y = x2 + cos x
A.E. is m2 – 2m + 3 = 0
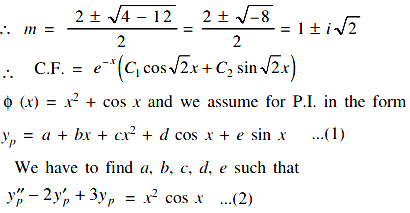
From (1), we obtain
y′p = b + 2cx – dsin x + e cos x
y′′p = 2c – d cos x – e sin x
Hence (2) becomes,
(2c – d cos x – e sin x) – (2b + 4cx – 2d sin x + 2e cos x) + (3a + 3bx + 3cx2 + 3d cos x + 3e sin x) = x2 + cos x
Comparing both sides, we obtain
2c – 2b + 3a = 0 ...(3)
– 4c + 3b = 0 ...(4)
3c = 1 ...(5)
2d – 2e = 1 ...(6)
2d + 2e = 0 ...(7)
Solving these equations, we get
