Question

In an increasing geometric progression of positive terms, the sum of the second and sixth terms is \( \frac{70}{3} \) and the product of the third and fifth terms is 49 . Then the sum of the \( 4^{\text {th }}, 6^{\text {th }} \) and \( 8^{\text {th }} \) terms is equal to : 

(1) 96

(2) 91

(3) 84

(4) 78

Answer 1

The correct option is (2) 91.

Let's denote the first term of the geometric progression by a and the common ratio by r. The terms of the geometric progression can be written as follows:

First term: a

Second term: ar

Third term: (ar²)

Fourth term: (ar³)

Fifth term: (ar⁴)

Sixth term: (ar⁵)

Eighth term: (ar⁷)

We are given two key pieces of information:

1. The sum of the second and sixth terms is \(\frac{70}{3}\):

ar + ar⁵ = \(\frac{70}{3}\)

2. The product of the third and fifth terms is 49:

(ar²)⋅(ar⁴) = 49

a²r⁶ = 49

a² = \(\frac{49}{r^5}\)

a = \(\frac{7}{r^3}\)

Substituting a = \(\frac{7}{r^3}\) into the first equation:

Multiply through by 3x to clear the denominator:

21 + 21x² = 70x

Rearrange into a standard quadratic equation:

21x² − 70x + 21 = 0

Divide by 7 to simplify:

3x² − 10x + 3 = 0

Solve this quadratic equation using the quadratic formula:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)

Where a = 3, b = −10, and c = 3. Thus:

Since x = r² and r is positive, we get r = √3 or r = 1/√3. We need to choose the value that results in positive, increasing terms:

If r = √3:

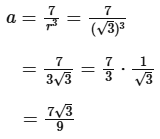
Now we can determine the sum of the 4th, 6th, and 8th terms:

Adding these together:

(4th + 6th + 8th terms) = 7 + 21 + 63 = 91

Therefore, the sum of the 4th, 6th, and 8th terms is 91.