Since we can ignore the height of the thrower’s hand above the ground, the launch point and the point of impact can be taken to be at the same height. We take the origin of the coordinate axes at the launch point. Since the distance covered by the hammer is the range, it is equal to the hammer’s range for θ0 = 450 . Thus we have from Eqn.(4.7):
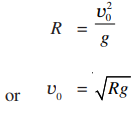
It is given that R = 19.6 m. Putting g = 9.8 ms–2 we get

The maximum height and time of flight are given by Eqns. (4.5) and (4.6), respectively. Putting the value of v0 and sin θ0 in Eqns. (4.5) and (4.6), we get

Now that you have studied some concepts related to projectile motion and their applications, you may like to check your understanding. Solve the following problems.