Question

A man in a boat sets out across a river from point A (Fig.). If he follows a course perpendicular to the river bank he will land 10 min later at point situated C/120 m downstream from point B. If he follows a course upstream at some angle a to line AB (AB is perpendicular to the banks of the river) he will land at point B in 12.5 min. Find the width l of the river, the speed u of the boat relative to the water, the velocity v of the river, and the angle a. The speed of the boat was constant throughout. 

Answer 1

Answer: l = 200m, u = 20m/min, v = 12 m/min, a = 36°52'.  

Explanation:

The motion of the boat in both cases is composed of its motion relative to the water and the motion of the water relative to the shore.

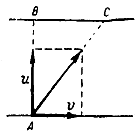
First case (Fig.): The boat moves along the river with a velocity v, and when it crosses with the current, it travels a distance

l₁ = vt₁. (1)

The motion across the river takes place with a velocity u for a distance

l₂ = ut₁   (2)

Second case (Fig.): The velocity of the boat along the river is zero, i.e.

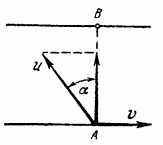
usinα  = v (3)

The velocity across the river is ucosα. and the distance l₂ travelled during the crossing is

l₂ = (ucosα)t₂.  (4)

Solving equations (1), (2), (3), (4), we obtain