Question

Determine the current in the 4-Ω branch in the circuit shown in Fig..

Answer 1

The three loop currents are as shown in Fig. 

For loop 1, we have 

− 1 (I₁ −I₂) − 3 (I₁ −I₃) − 4I₁ + 24 = 0 

or 8I₁ −I₂ − 3I₃ = 24 ...(i) 

For loop 2, we have 12 − 2I₂ − 12 (I₂ −I₃) − 1 (I₂ −I₁) = 0 

or I₁ − 15I₂ + 12I₃ = − 12 ...(ii) 

Similarly, for loop 3, we get 

− 12 (I₃ −I₂) − 2I₃ − 10 − 3(I3 −I₁) = 0 or 3I₁ + 12I₂ − 17I₃ = 10 ...(iii) 

Eliminating I₂ from Eq. (i) and (ii) above, we get, 119I₁ − 57I₃ = 372 ...(iv) 

Similarly, eliminating I₂ from Eq. (ii) and (iii), we get, 57I₁ − 111I₃ = 6 ...(v) From (iv) and (v) we have, 

I₁ = 40,950/9,960 = 4.1A 

Determinants 

The three equations as found above are 

8I₁ −I₂ − 3I₃ = 24 

I₁ − 15I₂ + 12I₃ = − 12 

3I₁ + 12I₂ − 17I₃ = 10

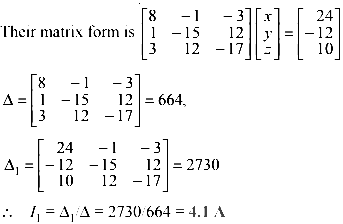
Using Mesh Resistance Matrix 

For the network of Fig., values of self resistances, mutual resistances and e.m.f’s can be written by more inspection of Fig.. 

R₁₁ = 3 + 1 + 4 = 8 Ω ; R₂₂ = 2 + 12 + 1 = 15Ω ; R₃₃ = 2 + 3 + 12 = 17Ω 

R₁₂ = R₂₁ = − 1; R₂₃ = R₃₂ = − 12 ; R₁₃ = R₃₁ = − 3 

E₁ = 24 V ; E₂ = 12 V ; E₃ = − 10 V 

The matrix form of the above three equations can be written by inspection of the given network as under :-

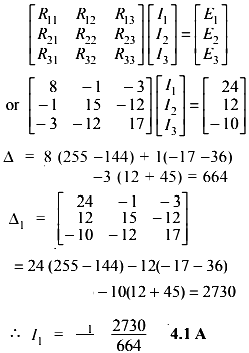
It is the same answer as found above.