Principle:
(i) Every point on a given wavefront may be regarded as a source of new disturbance.
(ii) The new disturbances from each point spread out in all directions with the velocity of light and are called the secondary wavelets.
(iii) The surface of tangency to the secondary wavelets in forward direction at any instant gives the new position of the wavefront at that time. Let us illustrate this principle by the following example:
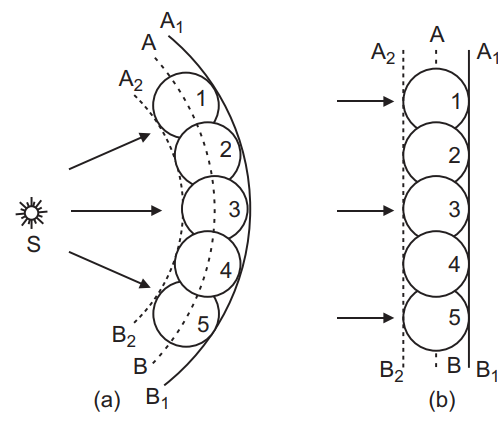
Let AB shown in the fig. be the section of a wavefront in a homogeneous isotropic medium at t = 0. We have to find the position of the wavefront at time t using Huygens’ principle. Let v be the velocity of light in the given medium.
(a) Take the number of points 1, 2, 3, … on the wavefront AB. These points are the sources of secondary wavelets.
(b) At time t the radius of these secondary wavelets is vt. Taking each point as centre, draw circles of radius vt.
(c) Draw a tangent A1B1 common to all these circles in the forward direction.
Propagation of wavefront from a point source: When monochromatic light is made incident on a single slit, we get diffraction pattern on a screen placed behind the slit. The diffraction pattern contains bright and dark bands, the intensity of central band is maximum and goes on decreasing on both sides.
Let AB be a slit of width ‘a’ and a parallel beam of monochromatic light is incident on it. According to Fresnel the diffraction pattern is the result of superposition of a large number of waves, starting from different points of illuminated slit.
Let θ be the angle of diffraction for waves reaching at point P of screen and AN the perpendicular dropped from A on wave diffracted from B. The path difference between rays diffracted at points A and B,

To find the effect of all coherent waves at P, we have to sum up their contribution, each with a different phase. This was done by Fresnel by rigorous calculations, but the main features may be explained by simple arguments given below:
At the central point C of the screen, the angle θ is zero. Hence the waves starting from all points of slit arrive in the same phase. This gives maximum intensity at the central point C. If point P on screen is such that the path difference between rays starting from edges A and B is λ, then path difference
asinθ = λ = sinθ = λ/a
If angle θ is small, sinθ = θ = λ/a ...(ii)

The intensity of secondary maxima decreases with increase of order n because with increasing n, the contribution of slit decreases.
For n = 2, it is one-fifth, for n = 3, it is one-seventh and so on.