Question

The total speed v₁ of a projectile at its greatest height is \(\sqrt \frac {6}{7}\)of its speed v₂ at half its greatest height. Find the angle of projection.

Answer 1

Velocity at the highest point = ucosθ = v₁

H_max = \(\frac {u^2sin^2\theta}{2g}\)

Using v = u - 2gh

At h = \(\frac{H_{(max)}}{2},\)vertical component of v₂ is given by

v_2y² = u²sin²θ - 2g x \(\frac{H_{(max)}}{2}\)

v_2y² = u² sin²θ - g \((\frac {u^2sin2\theta}{2g})\)

⇒ v = \(\frac {u^2sin^2\theta}{2}\)

Horizontal component v₂ is

v_2x = v₁ = ucosθ

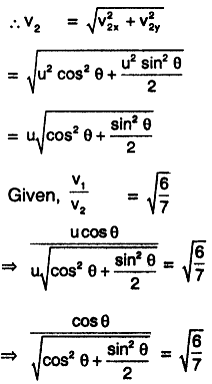
Squaring both sides,

⇒ 7 cos²θ = 6 cos²θ + 3 sin²θ

⇒ cos²θ = 3 sin²θ

⇒ tan²θ = \(\frac {1}{3}\)

⇒ tanθ = ±\(\frac{1}{\sqrt3}\)

⇒ θ = ± 30°

θ = 30°