Question

State and prove parallelogram law of vector addition. Discuss some special cases.

Answer 1

Let P and Q be two vectors acting simultaneously at a point and represented both in magnitude and direction by two adjacent sides OA and OD of a parallelogram OABD as shown in figure.

Let θ be the angle between P and Q and R be the resultant vector. Then, according to parallelogram law of vector addition, diagonal OB represents the resultant of P and Q.

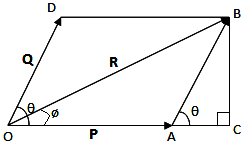
So, we have

R = P + Q

Now, expand A to C and draw BC perpendicular to OC.

From triangle OCB,

OB² = OC² + BC²

Or, OB² = (OA + AC)² + BC²  ......(i)

In triangle ABC,

cos \(\theta\) = \(\frac{AC}{AB}\)

Or, AC = AB cos\(\theta\)

or, AC = OD  cos\(\theta\) = Q  cos\(\theta\) [\(\because\) AB = OD = Q]

Also, 

 cos\(\theta\) = \(\frac{BC}{AB}\) 

or, BC = AB sin \(\theta\)

or, BC = OD sin \(\theta\) = Q sin \(\theta\) [\(\because\) AB = OD = Q]

Substituting value of AC and BC in (i), we get

which is the magnitude of resultant.

Let \(\phi\) be the angle made by resultant R with P. Then,

From triangle OBC,

which is the direction of resultant.

Special cases: (a) When two vectors are acting in same direction:

Thus, the magnitude of the resultant vector is equal to the sum of the magnitude of the two vectors acting in the same direction and their resultant acts in the direction of P and Q.

(b) When two vectors act in the opposite directions:

Thus, the magnitude of the resultant of two vectors acting in the opposite direction to the difference of the magnitude of two vectors and it acts in the direction of bigger vectors.

(c) If two vectors act perpendicular to each other: