Question

Calculate the moment of inertia of a thin rod about an axis perpendicular to the length and passing through one edge.

Answer 1

Moment of Inertia of a Thin Rod

(a) Moment of Inertia of a Thin Rod about the Axis Perpendicular to the Length and Passing through the Center.
Take a uniform thin rod AB whose mass is M and length is l. YY’ axis passes through the center of the rod and perpendicular to the length of the rod. We have to calculate the moment of inertia about this axis. YY’.

Fig: Moment of Inertia of a thin rod about the perpendicular axis along its length

Suppose, small piece dx is at a distance x from the YY’ axis. Hence, mass of length dx is = \(\left(\frac{M}{l}\right)\) dx
The moment of inertia of small piece about the YY’ axis
dl = \(\left[\left(\frac{M}{l}\right) d x\right] x^{2}\)
Therefore, the moment of inertia of the complete rod about the YY’ axis.

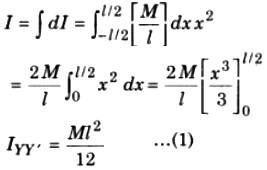
(b) Moment of Inertia about the axis perpendicular to the the length and passing through the Corner
If I_CD is the moment of inertia about the axis CD perpendicular to the length of a thin rod and passing through the point A then, by theorem of parallel axis;
I_CD = I_YY’ + Md²
= \(\frac{M l^{2}}{12}+M\left(\frac{l}{2}\right)^{2}\)
I_CD = \(\frac{M l^{2}}{3}\) ……………….. (2)