Question

Evaluate the integral: ∫e^√x dx

Answer 1

Consider √x = t

We get

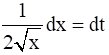
It can be written as

dx = 2 √x dt

where dx = 2t dt

We can replace it in the equation

∫e^√x dx = ∫e^t 2t dt

So we get

= 2 ∫t e^t dt

Consider the first function as t and second function as e^t

By integration w.r.t. t

= 2 (t e^t – ∫1. e^t dt)

We get

= 2 (t e^t – e^t) + c

Taking e^t as common

= 2 e^t(t – 1) + c

Substituting the value of t we get

= 2 e^√x(√x – 1) + c