Question

Draw graphs of x- 2y = 4, 2x – 4y = 12 on the same co-ordinate plane. Observe it. Think of the relation between the coefficients of x, coefficients of y and the constant terms and draw the inference.

Answer 1

i    x = 2y = 4 

∴ 2y = x - 4 

∴  y = \(\frac{x-4}{2} \)

x	0	2	-2	4
y	-2	-1	-3	0
(x,y)	(0,-2)	(2,-1)	(-2,-3	(4,0)

 2x - 4y = 12

∴ x - 2y = 6   .........[Dividing both sides by 2]

∴  2y = x - 6

∴   y= \(\frac{y-6}{2} \)

x	0	-2	2	4
y	-3	-4	-2	-1
(x,y)	(0,-3)	(-2,-4)	(2,-2	(4,-1)

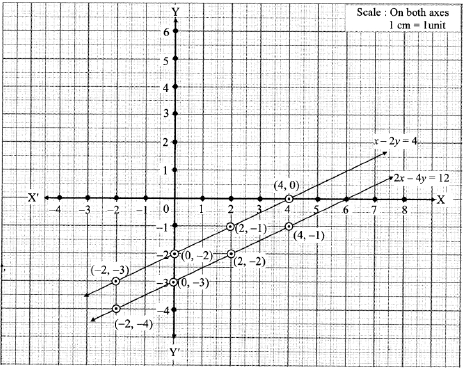
ii. Ratio of coefficients of x =\(\frac{1}{2} \)

Ratio of coefficients of y = \(\frac{-2}{-4} \)=\(\frac{1}{2} \)

Ratio of constant terms =\(\frac{4}{12} \) =\(\frac{1}{3} \)

∴ Ratio of coefficients of x = ratio of coefficients of y ratio of constant terms

iii. If ratio of coefficients of x = ratio of coefficients of y ≠ ratio of constant terms, then the graphs of the two equations will be parallel to each other.

Condition of consistency in Equations: