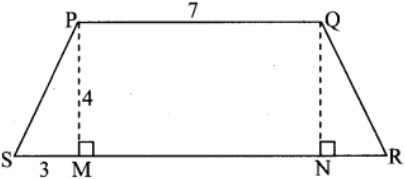
PQRS is an isosceles trapezium.
l(PQ) = 7 cm, seg PM ⊥ seg SR,
l(SM) = 3 cm, l(PM) = 4cm
Draw seg QN ⊥ seg SR.
In PMNQ, seg PQ || seg MN
∠PMN = ∠QNM = 90°
∴ PMNQ is a rectangle.
Opposite sides of a rectangle are congruent.
∴ l(PM) = l(QN) = 4 cm and
l(PQ) = l(MN) = 7 cm
In ∆PMS, m∠PMS = 90°
∴ [l(PS)]2 = [l(PM)]2 + [l(SM)]2 … [Pythagoras theorem]
∴ [l(PS)]2 = (4)2 + (3)2
∴ [l(PS)]2 = 16 + 9 = 25
∴ l(PS) = √25 = 5 cm …[Taking square root of both sides]
PQRS is an isosceles trapezium.
∴ l(PS) = l(QR) = 5 cm
In ∆QNR, m ∠QNR = 90°
∴ [l(QR)]2 = [l(QN)]2 + [l(NR)]2 … [Pythagoras theorem]
∴ (5)2 = (4)2 + [l(NR)]2
∴ 25 = 16 + [l(NR)]2
∴ [l(NR)]2 = 25 – 16 = 9
∴ l(NR) = √9 = 3 cm …[Taking square root of both sides]
l(SR) = l(SM) + l(MN) + l(NR)
= 3 + 7 + 3 = 13 cm
Area of a trapezium = (1/2) x sum of lengths of parallel sides x height
∴ A(PQRS) = (1/2) x [l(PQ) + l(SR)] x l(PM)
= (1/2) x (7+ 13) x 4
= (1/2) x 20 x 4
= 40 sq.cm
∴ The area of PQRS is 40 sq. cm.