When a bar magnet (magnetic dipole) of dipole moment
Suppose an electron undergoes circular motion around the nucleus. The circulating electron in a loop is like current in a circular loop (since flow of charge is current). The magnetic dipole moment due to current carrying circular loop is
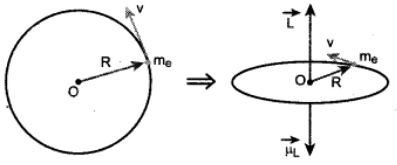
(a) Electron revolving in a circular orbit
(b) Direction of magnetic dipole moment vector and orbital angular momentum vector are opposite.
\(\vec {µ_L}\) = \(\vec A\) .........(1)
In magnitude, µ = I A
If T is the time period of an electron, the current due to circular motion of th electron is
I = \(\frac{-e}{T}\) ........... (2)
where -e is the charge of an electron. If R is the radius of the circular orbit and v is the velocity of the electron in the circular orbit, then
T = \(\frac{2πR}{v}\) .......... (3)
Using equation (2) and equation (3) in equation (1), we get

Where A = πR2 is the area of the circular loop. By definetion, angular moment of the electron about O is
\(\vec L = \vec R \times \vec P\)
In magnitude,
L = PR = mvR …….. (5)
Using equation (4) and equation (5), we get

The negative sign indicates that the magnetic moment and angular momentum are in opposite direction.
In magnitude,

The ration \(\frac{μ_L}{L}\) is a constant and also known as gyro-magnetic ration \(\frac{μ_L}{L}\). It must be noted that the gyro-magnetic ratio is a constant of proportionality which connects angular momentum of the electron and the magnetic moment of the electron. According to Neil’s Bohr quantization rule, the angular momentum of an electron moving in a stationary orbit is quantized, which means,
I = nh = n\(\frac {h}{2π}\)
where, h is the planck’s constant (h = 6.63 x 10-34 J s) and number n takes natural numbers (i.e., n = 1,2,3,…..). Hence,

µL = n x 9.27 x 10-24 A m2
The minimum magnetic moment can be obtained by subsituting by sustituting n = 1,

is called Bohr magneton. This is a convenient unit with which one can measure atomic magnetic moments.