Question

A particle moves along a line according to the law s(t) = 2t³ – 9t² + 12t – 4, where t ≥ 0. 

(i) At what times the particle changes direction? 

(ii) Find the total distance travelled by the particle in the first 4 seconds. 

(iii) Find the particle’s acceleration each time the velocity is zero.

Answer 1

(i) s = f(t) = 2t³ – 9t² + 12t – 4 

V = f'(t) = 6t² – 18t + 12

V = 0 ⇒ 6(t² - 3t – 2) = 0 

(t – 1)(t – 2) = 0 

t = 1, 2 

When t < 1, (say t = 0.5) 

V = 6(0.25 – 1.5 + 2) = +ve 

When 1 < t < 2, (say t = 1.5) 

V = 6(2.25 – 4.5 + 2) = - ve 

When t > 2, (say t = 3) 

V = 6(9 – 6 + 2) = +ve 

So the particle changes its direction when t lies between 1 and 2 secs.

(ii) The distance travelled in the first 4 seconds is 

|s(0) – s(1)| + |s(1) – s(2)| + |s(2) – s(3)| + |s(3) – s(4)| 

Here, s(t) = 2t³ – 9t² + 12t – 4 

s(0) = -4 

s(1) = 1 

s(2) = 0 

s(3) = 5 and 

s(4) = 28 

∴ Distance travelled in first 4 seconds 

= |-4 – 1| + |1 – 0| + |0 – 5| + |5 – 28|

= 5 + 1 + 5 + 23 = 34 m

(iii) 

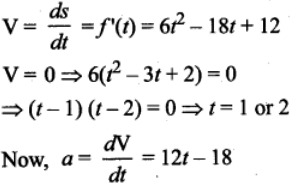
a(at V = 0) is ‘a’ at t = 1 and 2 

Now a(at t = 1) = 12 – 18 = -6m/sec² 

a(at t = 2) = 24 – 18 = 6m/sec²