When a body is pushed at an arbitrary angle θ (0 to\(\frac{π}{2}\)), the applied force F can be resolved into two components as F sin θ parallel to the surface and F cos θ perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is no acceleration along the vertical direction the normal force N is equal to
Npush = mg + F cos θ ………. (1)
As a result the maximal static friction also increases and is equal to

Equation (2) shows that a greater force needs to be applied to push the object into motion.

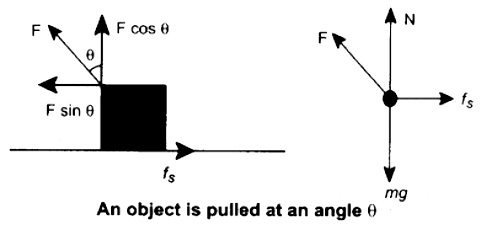
When an object is pulled at an angle 0, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is
Npull = mg – F cos θ ….. (3)