Question

In a sphere of radius 2 cm a cone of height 3 cm is inscribed. What is the ratio of volumes of the cone and sphere ?

Answer 1

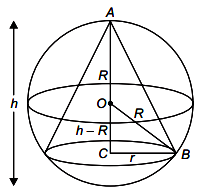
Given, radius of sphere (R) = 2 cm. Height of cone (h) = 3 cm. 

Point O is the centre of the sphere. 

∴ OA = OB = R, AC = h 

⇒ OC = AC – OA = h – R

Hence, in rt. ΔORC, r² = R² – (h – R)², where r is the radius of the cone 

= 2² – (3 – 2)² = 4 – 1 = 3

r = \(\sqrt3.\)

∴ \(\frac{\text{Volume of cone}}{\text{Volume of sphere}} = \) \(\frac{\frac13πr^2h}{\frac43πR^3}\) = \(\frac{(\sqrt3)^2\times3}{4\times2^3} = 9 : 32.\)