Question

Find the range of values of x which satisfy x² + 6x – 27 > 0, –x² + 3x + 4 > 0 simultaneously.

Answer 1

\(x\)² + 6\(x\) – 27 > 0    ⇒ (\(x\) + 9) (x – 3) > 0      ⇒ \(x\) = –9, 3 

By the method of intervals we see that (\(x\) + 9) (\(x\) – 3) is positive when \(x\) < – 9 and \(x\) > 3 

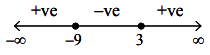
\(x\)² + 6\(x\) – 27 > 0 ⇒ x∈ (–∞, –9) ∪ (3, ∞)          …(i) 

Now   –\(x\)² + 3\(x\) + 4 > 0     ⇒ \(x\)² – 3\(x\) – 4 < 0 ⇒ (\(x\) – 4) (\(x\) + 1) < 0 

∴ (\(x\) – 4) (\(x\) + 1) = 0 ⇒ \(x\) = – 1, 4 

∴ The expression (\(x\) – 4) (\(x\) + 1) is negative when x lies between –1 and 4. 

∴ \(x\)∈ (–1, 4)               …(ii) 

∴ (i) and (ii)           ⇒ \(x\) ∈ (3, 4).