(b) \(\frac{12\sqrt3}{7}\)
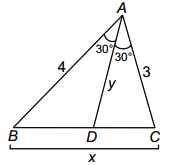
Let BC = x and AD = y, then as per bisector theorem,
\(\frac{BD}{DC}= \frac{AB}{AC}\) = \(\frac{4}{3}\)
∴ BD = \(\frac{4x}{7}\) and DC = \(\frac{3x}{7}\)
Now in ΔABD using cosine rule,
cos 30º = \(\frac{AB^2+AD^2-BD^2}{2\times{AB}\times{AD}}\)

In ΔACD using the cosine rule,
cos 30º = \(\frac{AC^2+AD^2-CD^2}{2\times{AC}\times{AD}}\)

Also in ΔABC, cos 60º = \(\frac{AB^2+AC^2-BC^2}{2\times{AB}\times{AC}}\)
⇒ \(\frac{1}{2}\) = \(\frac{16+9-BC^2}{2\times4\times3}\) ⇒ 12 = 25 - BC2
⇒ BC2 = 13 ⇒ x2 = 13
∴ Subtracting eqn (ii) from (i), we get
\(\sqrt3\,y=7-\frac{7x^2}{49}=7-\frac{7\times13}{49}=7-\frac{13}{7}=\frac{49-13}{7}=\frac{36}{7}\)
⇒ y = \(\frac{36}{7\times\sqrt3}\) = \(\frac{12\sqrt3}{7}\).