Consider ΔABC with vertices A, B, C and sides BC = α, AC = β and AB = γ
Let the position vectors of A, B and C be \(\vec a,\vec b\) and \(\vec c\) respectively.
Let D and E (with position vectors \(\vec d\) and \(\vec e\)) be points on BC and AB such that AD and CE are the bisectors of ∠A and ∠C. Let, AB and CE meet at point I.
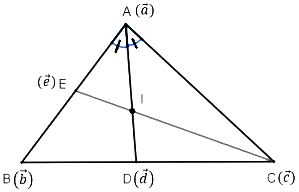
Observe from the figure that D divides BC in the ratio BD:DC.
Using the angular bisector theorem, we know that the angle bisector of an angle in a triangle bisects the opposite side in the ratio equal to the ratio of the other two sides.
⇒ \(\cfrac{BD}{DC}=\cfrac{AB}{AC}=\cfrac{\gamma}{\beta}\) (from our initial assumption)
Recall the position vector of point P which divides AB, the line joining points A and B with position vectors \(\vec a\) and \(\vec b\) respectively, internally in the ratio m : n is

From angular bisector theorem above, we had \(\cfrac{BD}{DC}=\cfrac{AB}{AC}\)
Adding 1 to both sides,

In addition, as CI is the angular bisector of ∠C in ΔACD, using the angular bisector theorem,
we have

So, I divides AD in the ratio (β + γ) : α.
Let the position vector of I be \(\vec {\text x}\)
Using the aforementioned section formula, we can write

Now, observe E divides AB in the ratio AE : EB.
⇒ \(\cfrac{AE}{EB}=\cfrac{AC}{BC}=\cfrac{\beta}{\alpha}\)(from angular bisector theorem)
So, \(\vec e=\cfrac{\beta\vec b+\alpha \vec a}{\beta+\alpha}\) (using section formula)
By doing similar calculations as above for ∠C, we get

Observe that \(\vec{\text x}=\vec y\) meaning the point I with position vector \(\cfrac{\alpha\vec a+\beta\vec b+\gamma \vec c}{\alpha+\beta+\gamma}\) lies on both AB and CE.
Similarly, it can be shown that this point I also lies on the third angular bisector.
Thus, the internal bisectors of the angles of a triangle are concurrent with the point of concurrency given by the position vector \(\cfrac{\alpha\vec a+\beta\vec b+\gamma \vec c}{\alpha+\beta+\gamma}\) where α, β and γ are sides of the ΔABC opposite to the vertices A, B and C.