Let vector p = 2i + 3j + k and vector q = i + 2j + k be two vectors. if a vector vector r = (αi + βj + γk) is perpendicular to each

Question

Let \(\vec P = 2\hat i + 3\hat j + \hat k\) and \(\vec q = \hat i + 2\hat j + \hat k\)  be two vectors. If a vector  \(\vec r = (\alpha \hat i + \beta \hat j + \gamma \hat k)\) is perpendicular to each of the vectors  \((\vec p + \vec q)\)  and \((\vec p - \vec q)\) , and | \(\vec r\) | \(\sqrt{3}\)  , then |α| + |β| + |γ| is equal to ____.

Answer 1

\(\vec P = 2\hat i + 3\hat j + \hat k\) (given)

\(\vec q = \hat i + 2\hat j + \hat k\)

Now \((\vec p + \vec q)\) x \((\vec p - \vec q)\) = \(\begin{vmatrix} \hat i & \hat j & \hat k \\[0.3em] 3 & 5 & 2 \\[0.3em] 1 & 1 & 0 \end{vmatrix}\)

= - 2\(\hat i\) - 2\(\hat j\) - 2\(\hat k\)

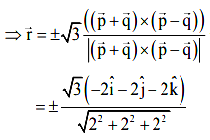
\(\vec r = \pm\)(- \(\hat i\) - \(\hat j\) - \(\hat k\))

According to question 

\(\vec r\) = α\(\hat i\) + β\(\hat j\) + γ\(\hat k\)

So |α| = 1, |β| = 1, |γ| = 1

\(\Rightarrow\) |α| + |β| + |γ| = 3