A spherical shape has the minimum surface area- to-volume ratio of all geometric forms. When two drops of a liquid are brought in contact, the cohesive forces between their molecules coalesces the drops into a single larger drop. This is because, the volume of the liquid remaining the same, the surface area of the resulting single drop is less than the combined surface area of the smaller drops. The resulting decrease in surface energy is released into the environment as heat.
Proof : Let n droplets each of radius r coalesce to form a single drop of radius R. As the volume of the liquid remains constant, volume of the drop = volume of n droplets
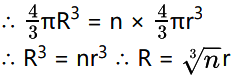
Surface area of n droplets = n × πR2
Surface area of the drop = 4πR2 = n2/3 × πR2
\(\therefore\)The change in the surface area = surface
area of drop – surface area of n droplets = πR2 (n2/3 – n)
Since the bracketed term is negative, there is a decrease in surface area and a decrease in surface energy.