Question

`(A)(C_(10)H_(16))overset(Reductive or o x idative)underset(ozonolysis)rarr(B)(C_(5)H_(8)O)`
`(A)` reacts with one equivalent of `H_(2)//Pd`
`a.` Both `(A)` and `(B)` are resolvable.
b. Both `(A)` and `(B)` are irresolvable.
c. (B) is resolvable but `(A)` is not.

Answer 1

`i.` `D.U.` in `(A)=((2n_(C)+2)-n_(H))/(2)=3^(@)(` one `(C=C)+`two rings `)`
`ii.` `D.U. `in `(B)=2^(@)[`one `(gtC=O)` group and one ring `]`
`iii.` Since `(A)` reacts with one equivalent of `H_(2)`, one `(C=C)` and two rings of five `C` atoms or four `C` atoms with one `(=Me)` group in each ring.
`iv.` Moreover, oxidative and reductive oxonolyses give the same product, so `(B)` must be a cyclic ketone.
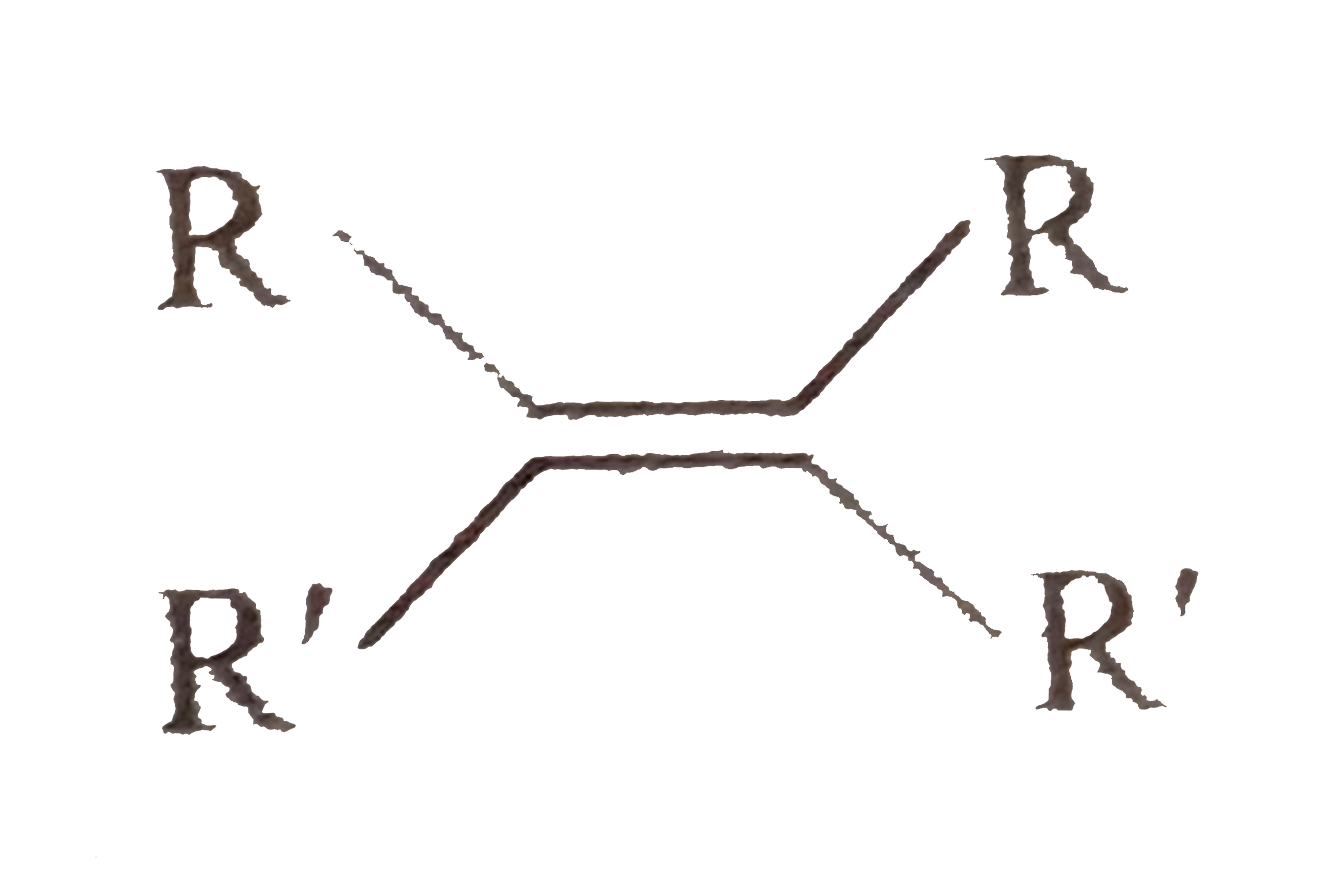
Possibilities are `:[` alkene of the type and `(C=C)` exocyclic to both rings. `]`.
`a.`
`b.` Both `(A)` and `(B)` are optically inactive` (` non`-` resolvable `).`

`c.` `(A)` is non`-` resolvable but `(B)` is resolvable. ltbr.