Gravitation class 9 Science notes

Question

Revise for exam with Gravitation class 9 Science notes avliable here.

Answer 1

Important topics covered under Gravitation class 9 notes:

• What is gravitation?
• Universal law of gravitation
• Free Fall
• Acceleration due to gravity
• Motion of object under the influence of gravitational force of earth.
• Mass
• Weight
• Thrust and pressure
• Pressure in fluids
• Buoyancy
• Float or sink
• Archimedes’ Principle
• Relative Density

---

What is gravitation?

• The natural phenomenon which allows every particle of this universe which has mass and energy to attract each other.
• When any object on the earth is attracted by the earth towards its centre then it is said to be Gravitation of earth.
• If we release a ball at some height above the earth it starts accelerating towards the earth. Which means that ball is attracted by the earth while ball also attracts the earth.

Universal law of Gravitation by Sir. Newton:

• According to universal law of gravitation, every particle having mass attracts other particle with a force which is directly proportional to the product of masses and is inversely proportional to the square of distance between them.
• This law was proposed by Sir. Issac Newton in 1687 about the force of attraction between the two bodies in universe and is named as Newton’s law of gravitation.

Mathematical formulation of universal law of gravitation:

• Let the mass of two different objects be (M) and (m) and separated by a distance (r), then force of gravity between them are:

  F ∝ M × m
  F ∝ \(\frac{1}{d^{2}}\)

  F ∝ \(\frac{Mm}{d^{2}}\)
  F = G\(\frac{Mm}{d^{2}}\)

  Here G is the Universal gravitational constant.

• The value of G is 6.67×10^-11 Nm²/Kg²
• In the higher section, you will read more about gravitation In this section notes for class 9 level is there.

Relation between Newton’s third law of motion and gravitation:

Newton’s third law of motion	Gravitation
Every particle of this universe exerts equal and opposite force on each other but in opposite direction.	Every Mass attracts other mass of this universe.
As per third law, the ball also attracts then earth.	When a ball is dropped it freely falls towards earth which means earth attracts the ball.
The force (F=ma) at which ball attracts the earth is much low as the mass of ball is much lesswhen compared to the earth.	But the force at which earth attracts the ball is quiet larger.
The acceleration of earth towards ball is1.65 × 10-24 m/s2	The acceleration due to gravity of earth on ball is 9.8 m/s2

Importance of Universal law of Gravitation:

• The force of gravitation binds object to the earth.
• It deprives the motion of moon and other natural satellites around the earth.
• The motion of different planets around the sun is due to gravitation.
• The formation of sea tides are due to the gravitational pull of moon.

Free fall motion:

• When any object falls under the influence of force of gravity only then it is said to be free fall.
• The velocity of a body under free fall continuously increases.

Acceleration due to gravity:

• The acceleration of the object under free fall is said to be acceleration due to gravity.
• Acceleration due to gravity is denoted by
• The unit of g is same as the acceleration i.e. m/s².
• The value of g is 9.8 m/s².
• This acceleration is always directed towards the centre of earth.

Mathematical calculation of acceleration due to gravity(g):

• From second law of motion,
  F = mg (As a = g) …..(i)
  But, from universal law of gravitation
  F = G\(\frac{Mm}{d^{2}}\) …..(ii)
  From Eq. (i) and (ii)
  mg = G\(\frac{Mm}{d^{2}}\)
  g = \(\frac{GM}{d^{2}}\)
  As we know the value of
  G= 67×10^-11 Nm²/Kg²
  M_e = 6 x 10²⁴ Kg
  d = 6.37x10⁶m
  So by putting the given value in equation of g.
  g = \(\frac{6.67×10^{-11} × 6 × 10^{24}}{({6.37 × 10^{6}}) ^{2}}\) = 9.8m/s²

Relation between g(acceleration due to gravity) and G(Gravitational constant):

• g = G\(\frac{M}{r^{2}}\)

Difference between g and G:

Acceleration due to gravity (g)	Gravitational constant (G)
The value of g is 9.8m/s2.	The value of G is 6.67 x 10-11Nm2/Kg2.
It is a vector quantity.	It is a scalar quantity.
The unit of g is m/s2.	The value of G is Nm2/Kg2.
Its value varies from place to place.	It’s value is constant everytime.

Answer 2

Equation of motion under gravity:

• If u = initial velocity
  v is final velocity
  t is time taken
  a is acceleration
  g is acceleration due to gravity, then

Equation with acceleration	Equation having acceleration due to gravity
v = u + at	v = u + gt
s = ut + \(\frac{1}{2}\)at2	s = ut + \(\frac{1}{2}\)gt2
v2 = u2 + 2as	v2 = u2 + 2gs

Remember* If the object is thrown upwards then the acceleration due to gravity will be negative (i.e. 9.8m/s²).

Mass:

• The quantity of matter contained in a body is called mass.
• It is scalar quantity as it has only magnitude not the direction.
• The SI unit of mass is kg.
• Mass of any object is always constant and doesn’t change from place to place.
• Mass of a body is usually denoted by m.
• Mass can’t be zero.

Weight:

• The magnitude of force by which any object is attracted towards the earth is called its weight.
• As we know that,
  F = ma
  Here a = g
  Thus, F = mg
  which is equal to weight
  *W = mg
• The SI unit of weight is
• The value of weight depends upon
• It is vector quantity.

Weight of an object at Moon:

• The moon also attracts any object toward its centre same as the earth but the gravitational pull is somewhat lower than the earth.
• The moon has lesser mass as compared to that of the earth.
• Due to this fact the moon exerts lesser force of attraction on objects.
• The ratio of weights of a body at the moon to earth is \(\frac{1}{6}\).

i.e. \(\frac{Weight \:of\: the \:object \:on \:the\: moon}{Weight \:of \:the\:object \:on \:the\:earth}\) = \(\frac{1}{6}\).

Difference between mass and weight:

Mass	Weight
Mass of any object is measured by its inertia.	Weight of a body is calculated by m x g.
Mass is the quantity of matter contained any object.	Weight is the force acting on any object.
The SI unit of Mass is Kg.	The SI unit of weight is N.
Mass is constant anywhere in the universe.	The value of weight changes with the value of g.
Mass is scalar quantity.	Weight is vector quantity.
Mass can’t be zero.	Weight can be zero at gravity free space.
It is denoted by m.	It is denoted by W.

Factors affecting the value of g:

• The radius of earth increases from pole to the equator. As we already know that earth is not a sphere.
• The value of g decreases as the value of distance of centre and surface of earth (radius) of earth increases.
• For calculation purpose we take a constant value of g at the surface of earth but at height above the earth we take g = G\(\frac{M}{d^{2}}\)

Thrust and Pressure:

• The force acting on an object perpendicular to the surface is said to be thrust.
• Thrust per unit area is called pressure.
• Pressure(P) = \(\frac{force}{Area}\) = \(\frac{F}{A}\)
• The unit of Pressure is N/m².
• The SI unit of Pressure is Pascal (Pa).
• Thus, pressure depends upon force applied as well as the area of surface at which it acts.

Pressure in Fluids:

• All liquids and gases are fluids.
• Fluids also have weight hence, they also exert pressure on base of walls of the container which it is kept.
• Pressure exerted in any confined mass of fluid is transmitted in all directions.

Buoyancy:

• The upthrust force experienced by a body when immersed in a fluid is said to be buoyant force.
• Buoyant force mostly acts in upward direction and it depends on the density of fluid.

Different conditions of Buoyancy:

• If gravitational pull of the earth on the surface of the object is less than the buoyant force exerted by fluid on the surface of the object, then object floats on the surface.
• If gravitational pull of the earth on the surface of the object is greater than the buoyant force exerted by fluid on the surface of the object, then object sinks in the fluid.

Answer 3

Density:

• Mass of any fluid per unit volume is said to be density of that fluid.
• If M is the mass and V is the volume of an object, then
  Density (d) = \(\frac{Mass}{Volume}\) = \(\frac{M}{V}\)
• The SI unit of density is Kg/m³

Density of different Material are:

Material	Density(gram/cm3)
Rubbing Alcohol	0.79
Lamp Oil	0.8
Baby Oil	0.83
Water	1.0
Milk	1.03
Liquid Soap	1.06
Corn Syrup	1.33
Maple Syrup	1.37
Honey	1.42

Archimedes principle:

• According to Archimedes’ Principle, when a body is immersed partially or wholly in a fluid it experience a force which is equal to the weight of the displaced fluid.

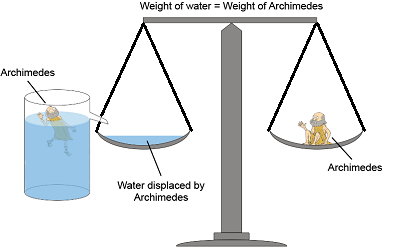
Applications of Archimedes’ Principle:

• By the use of Archimedes’ principle we can determine the relative density of a substance.
• It has a great application in designing ships and submarines.
• Lactometer are designed to measure for milk purity.
• Hydrometer are designed to measure the density of water.

Relative density or Specific gravity:

• The ratio of density of any substance to that of density of water is said to be relative density.
  Relative Density = \(\frac{Density\:of\:substance}{Density\:of\:water}\)
• Relative density has no unit as it is the ratio of similar quantities.
• The density of water at room temperature is 1g/cm³ this density is treated as a standard and density of any other material (usually liquids) is calculated relative to the density of water.

FAQ and Examples On Gravitation:

Q. What are the applications of Newton's Law of Gravitation?

Solution: There are several applications of Newton's law of gravitation. But one of the main application is to estimate masses of binary stars. A system of two stars orbiting round their common centre of mass is called binary star. Any irregularity in the motion of a star indicates that it might be another star or a planet going round the stars. This regularity in the motion of a star is called a wobble.

Q. Why is it difficult to hold a school bag having a strap made of a thin and strong string?

Solution: It is difficult to hold a bag having a strap made of a thin and strong string because the force of gravitation Bag exerts quiet large pressure on our shoulder. We already know that the pressure is inversly proportional to the surface area of the force action. If the surface area is smaller it will exert a greater force hence small contact surface of strip exerts a greater force.

Q. What is the magnitude of the gravitational force between the Earth and a 1 kg object on its surface? (Mass of the Earth is 6 × 10²⁴ kg and radius of the Earth is 6.4 × 10⁶ m).

Solution: As we know from the universal law of gravitation, gravitational force between two objects of masses M and m at a distance r from each other is given by:
F = G\(\frac{Mm}{r^{2}}\)

Here we are given with
G = 6.67 x 10^-11Nm²/Kg²
M= 6 × 10²⁴ kg
m= 1 Kg
r = 6.4 x 10² 
So, F = G\(\frac{6x10^{24} x 1}{{6.4 x 10^{2}}^{2}}\) = 9.8 N

Q. A ball is thrown vertically upwards with a velocity of 98 m/s. Calculate
(i) the maximum height to which it rises,
(ii) the total time it takes to return to the surface of the Earth.

Solution: 

(i) For the upward motion of the ball, we use the equation:
v² - u² = 2 gh
where,
u = Initial velocity of the ball = 98 m/s (Given)
v = Final velocity of the ball = 0 (At the highest point)
h = Maximum height attained by the ball
g = Acceleration due to gravity = -9.8 m/s² (Ball goes upwards opposite to the gravity)
Putting the values, we get
0 - (98)² = 2 × (-9.8) × h
h = 490 m

(ii) Let t be the time taken by the ball to reach the height 490 m, then to find t we use the following equation of motion:
v = u + g t
Putting the values, we get
0 = 98 + (-9.8) × t
0 = 98 - 9.8 t
98 = 9.8 t
t= 10 s
But, Time of ascent = Time of descent
Therefore, the total time taken by the ball to return = 10 + 10 = 20 s