In ΔABC, PQ||AB, P, Q are on BC and AC. If CQ : QA = 1 : 3 and CP = 4, then BC = (A) 8

Question

In ΔABC, \(\overline{PQ}||\overline{AB}\), P, Q are on BC and AC. If CQ : QA = 1 : 3 and CP = 4, then BC =

(A) 8

(B) 12

(C) 16

(D) 4

Answer 1

Correct option is (C) 16

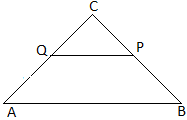
In \(\triangle ABC,\) QP || AB

\(\therefore\) \(\triangle CQP\sim\triangle CAB\)

\((\because\) Corresponding angles are equal as QP || AB)

\(\therefore\) \(\frac{CQ}{CA}=\frac{CP}{CB}\)    ______________(1)    (By properties of similar triangles)

Given that \(\frac{CQ}{QA}=\frac13\)

\(\Rightarrow QA=3CQ\)

\(\because CA=CQ+QA\)

\(=CQ+3CQ\)

\(=4CQ\)

\(\Rightarrow\) \(\frac{CQ}{CA}=\frac14\)

Then from (1), we obtain

\(\frac{CP}{BC}=\frac14\)

\(\Rightarrow BC=4CP\)

\(=4\times4=16\)     \((\because CP=4)\)

Answer 2

Correct option is: (C) 16