33. If the areas of two similar triangles are equal, prove that they are congruent.
Answer:
Let us assume two similar triangles as ∆ABC ∼ ∆PQR.

Given that, ar(∆ABC) = ar (∆PQR)
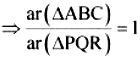
Putting this value in equation (!), we obatin

34. D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the area of ∆DEF and ∆ABC.
Answer:

D and E are the mid-points of ∆ABC.
∴ \(DE \parallel AC\, and \,DE = \frac{1}{2}AC\)
In ∆BED and ∆BCA,


35. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Answer:
Let us assume two similar triangles as ∆ABC ∼ ∆PQR.
Let AD and PS be the medians of these triangles.
∵ ∆ABC ∼ ∆PQR
\(\therefore \frac{AB}{PQ }=\frac{BC}{QR}= \frac{AC}{PR} ....(1)\)
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ……… (2)
Since AD and PS are medians,
∴ BD = DC = \(\frac{BC}{2}\)
And, QS = SR = \(\frac{QR}{2}\)
Equation (1) becomes
\(\frac{AB}{PQ }=\frac{BD}{QS}= \frac{AC}{PR} ....(3)\)
In ∆ABD and ∆PQS,
∠B = ∠Q [Using equation (2)]
And, \(\frac{AB}{PQ}= \frac{BD}{QS}\) [Using equation (3)]
∴ ∆ABD ∼ ∆PQS (SAS similarity criterion)
Therefore, it can be said that
\(\frac{AB}{PQ }=\frac{BD}{QS}= \frac{AD}{PS} ....(4)\)

From equations (1) and (4), we may find that
\(\frac{AB}{PQ }=\frac{BC}{QR}= \frac{AC}{PR} =\frac{AD}{PS}\)
And hence,
\(\frac{ar(\triangle ABC)}{ar(\triangle PQR)}= (\frac{AD}{PS})^2\)
36. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Answer:

Let ABCD be a square of side a.
Therefore, its diagonal = \(\sqrt{2a}\)
Two desired equilateral triangles are formed as ∆ABE and ∆DBF.
Side of an equilateral triangle, ∆ABE, described on one of its sides = a
Side of an equilateral triangle, ∆DBF, described on one of its diagonals = \(\sqrt{2a}\)
We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other. Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.

37. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
(A) 2 : 1
(B)1 : 2
(C) 4 : 1
(D) 1 : 4
Answer:

We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other.
Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.
Let side of ∆ABC = x
Therefore, side of \(\triangle BDE= \frac{x}{2}\)

Hence, the correct answer is (C).
38. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Answer:
If two triangles are similar to each other, then the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides of these triangles.
It is given that the sides are in the ratio 4:9.
Therefore, ratio between areas of these triangles = \((\frac{4}{9})^2 = \frac{16}{81}\)
Hence, the correct answer is (D).
39. Sides of triangles are given below. Determine which of them are right triangles? In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Answer:
(i) Given, sides of the triangle are 7 cm, 24 cm, and 25 cm.
Squaring the lengths of the sides of the, we will get 49, 576, and 625.
49 + 576 = 625
(7)2 + (24)2 = (25)2
Therefore, the above equation satisfies, Pythagoras theorem. Hence, it is right angled triangle.
Length of Hypotenuse = 25 cm
(ii) Given, sides of the triangle are 3 cm, 8 cm, and 6 cm.
Squaring the lengths of these sides, we will get 9, 64, and 36.
Clearly, 9 + 36 ≠ 64
Or, 32 + 62 ≠ 82
Therefore, the sum of the squares of the lengths of two sides is not equal to the square of the length of the hypotenuse.
Hence, the given triangle does not satisfies Pythagoras theorem.
(iii) Given, sides of triangle’s are 50 cm, 80 cm, and 100 cm.
Squaring the lengths of these sides, we will get 2500, 6400, and 10000.
However, 2500 + 6400 ≠ 10000
Or, 502 + 802 ≠ 1002
As you can see, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side.
Therefore, the given triangle does not satisfies Pythagoras theorem.
Hence, it is not a right triangle.
(iv) Given, sides are 13 cm, 12 cm, and 5 cm.
Squaring the lengths of these sides, we will get 169, 144, and 25.
Thus, 144 +25 = 169
Or, 122 + 52 = 132
The sides of the given triangle are satisfying Pythagoras theorem.
Therefore, it is a right triangle.
Hence, length of the hypotenuse of this triangle is 13 cm.