Question

NCERT Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations have solutions to all the queries one student might have.

NCERT Solutions Class 11 covers all important topics one needs for exam preparation.

• Need for complex numbers – there is numerous use of complex numbers in mathematics as well as in physics. Complex number can be used to solve zeros of a quadratic equation. If we encounter a negative in any square root in such places complex numbers can be used to simplify the zero. Complex numbers can be used in electronics and electromagnetism.

• Algebraic properties of complex numbers – for the complex numbers the properties of addition and multiplication are the same.
  • Closure property of addition – for any two complex numbers y₁ and y₂ the sum of y₁ + y₂ is also a complex number.
  • The commutative property – for any two complex numbers y₁ and y₂ we have y₁ + y₂ = y₂ + y₁
  • The associative property – for any two complex numbers y₁, y₂, and y₃ we have (y₁+y₂)+y₃ = y₁+(y₂+y₃)
  • The additive identity – there exists a complex number 0 = 0+0i such that, for every complex number y, y + 0 = 0 + y = y. the complex number 0 = 0+0i is called the additive identity of complex number.
  • The additive inverse – for every complex number y there exists a complex number –y such that y+(-y) = (-y)+y = 0. –y is called the additive inverse of z.

• Argand plane and polar representation of complex numbers – the complex number x+iy refers to the ordered pair (x,y) is geometrically represented as the unique point (x,y) in the XY- plane. For example, the complex number, 2+7i corresponds to the ordered pair (2,7) geometrically, and in the same way ordered pair -3+8i refers to the (-3,2).

• Statement of Fundamental Theorem of Algebra – every polynomial equation of degree n also has complex number coefficients has n number of roots or solutions.

• Solution of quadratic equations in the complex number system

• Square root of a complex number

NCERT Solutions Class 11 Maths is an important part of students’ preparation for their boards and competitive exam preparation.

Answer 1

NCERT Solutions Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations

1. Express the given complex number in the form a + ib: 

(5i) \(\left(-\frac{3}{5}i\right)\) 

Answer:

2. Express the given complex number in the form a + ib: 

i⁹ + i¹⁹

Answer:

3. Express the given complex number in the form a + ib: 

i^–39

Answer:

4. Express the given complex number in the form a + ib: 

3(7 + i7) + i(7 + i7)

Answer:

5. Express the given complex number in the form a + ib:

(1 – i) – (–1 + i6)

Answer:

(1 – i) – (–1 + i6) = 1 - i + 1 - 6i

= 2 - 7i

6. Express the given complex number in the form a + ib:

\(\left(\frac15+i\frac25\right)-\left(4+i\frac52\right)\)

Answer:

7. Express the given complex number in the form a + ib:

Answer:

8. Express the given complex number in the form a + ib: (1 – i)⁴

Answer:

9. Express the given complex number in the form a + ib:

\(\left(\frac13+3i\right)^3\) 

Answer:

10. Express the given complex number in the form a + ib:

\(\left(-2-\frac13i\right)^3\)

Answer:

11. Find the multiplicative inverse of the complex number 4 – 3i.

Answer:

Let z = 4 – 3i 

Then,

\(\overline z\) = 4 + 3i and \(|z|^2 = 4^2 +(-3)^2=16 +9 = 25\) 

Therefore, the multiplicative inverse of 4 – 3i is given by

12. Find the multiplicative inverse of the complex number √5 + 3i

Answer:

Let z = √5 + 3i

Then,

Therefore, the multiplicative inverse of √5 + 3i

13. Find the multiplicative inverse of the complex number –i

Answer:

Let z = –i

Then, \(\overline z\) = i and |z|² = 1² = 1

Therefore, the multiplicative inverse of –i is given by

14. Express the following expression in the form of a + ib.

Answer:

15. Find the modulus and the argument of the complex number z = -1 -i√3

Answer:

z = -1 -i√3

Let r cos θ = -1 and r sin θ = - √3

On squaring and adding, we obtain

Since both the values of sin θ and cos θ are negative and sinθ and cosθ are negative in III quadrant,

Argument = \(-(\pi-\frac{\pi}3)= \frac{-2\pi}{3}\)

Thus, the modulus and argument of the complex number -1 -√3 i are 2 and \(\frac{-2\pi}{3}\) respectively.

16. Find the modulus and the argument of the complex number z = -√3 + i

Answer:

z = -√3 + i

Let r cos θ = - √3 and r sin θ = 1

On squaring and adding, we obtain

Thus, the modulus and argument of the complex number -√3 + i are 2 and \(\frac{5\pi}{6}\) respectively.

17. Convert the given complex number in polar form: 1 – i

Answer:

1 – i 

Let r cos θ = 1 and r sin θ = –1 

On squaring and adding, we obtain

This is the required polar form.

Answer 2

18. Convert the given complex number in polar form: – 1 + i

Answer:

– 1 + i 

Let r cos θ = –1 and r sin θ = 1 

On squaring and adding, we obtain

It can be written,

This is the required polar form.

19. Convert the given complex number in polar form: – 1 – i

Answer:

– 1 – i 

Let r cos θ = –1 and r sin θ = –1 

On squaring and adding, we obtain

This is the required polar form.

20. Convert the given complex number in polar form: –3

Answer:

–3 

Let r cos θ = –3 and r sin θ = 0 

On squaring and adding, we obtain

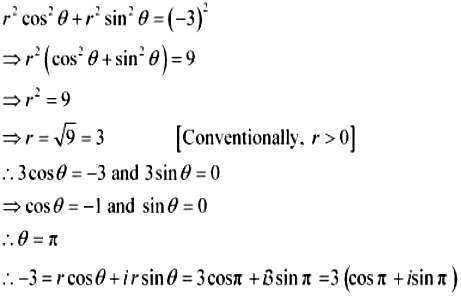
This is the required polar form.

21. Convert the given complex number in polar form:

√3 + i

Answer:

√3 + i

Let r cos θ = √3 and r sin θ = 1 

On squaring and adding, we obtain

This is the required polar form.

22. Convert the given complex number in polar form: i

Answer: 

i 

Let r cosθ = 0 and r sin θ = 1 

On squaring and adding, we obtain

This is the required polar form.

23. Solve the equation x² + 3 = 0

Answer: 

The given quadratic equation is x² + 3 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 1, b = 0, and c = 3 

Therefore, the discriminant of the given equation is

D = b² – 4ac = 0² – 4 × 1 × 3 = –12 

Therefore, the required solutions are

24. Solve the equation 2x² + x + 1 = 0

Answer: 

The given quadratic equation is 2x² + x + 1 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 2, b = 1, and c = 1 

Therefore, the discriminant of the given equation is

D = b² – 4ac = 1² – 4 × 2 × 1 = 1 – 8 = –7 

Therefore, the required solutions are

25. Solve the equation x² + 3x + 9 = 0

Answer:

The given quadratic equation is x² + 3x + 9 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 1, b = 3, and c = 9 

Therefore, the discriminant of the given equation is 

D = b² – 4ac = 3² – 4 × 1 × 9 = 9 – 36 = –27 

Therefore, the required solutions are

26. Solve the equation –x² + x – 2 = 0

Answer:

The given quadratic equation is –x² + x – 2 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = –1, b = 1, and c = –2 

Therefore, the discriminant of the given equation is 

D = b² – 4ac = 1² – 4 × (–1) × (–2) = 1 – 8 = –7 

Therefore, the required solutions are

27. Solve the equation x² + 3x + 5 = 0

Answer:

The given quadratic equation is x² + 3x + 5 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 1, b = 3, and c = 5

Therefore, the discriminant of the given equation is 

D = b² – 4ac = 3² – 4 × 1 × 5 =9 – 20 = –11

Therefore, the required solutions are

28. Solve the equation x² – x + 2 = 0

Answer:

The given quadratic equation is x² – x + 2 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 1, b = –1, and c = 2 

Therefore, the discriminant of the given equation is 

D = b² – 4ac = (–1)² – 4 × 1 × 2 = 1 – 8 = –7 

Therefore, the required solutions are

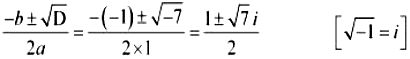
29. Solve the equation √2x² + x + √2 = 0

Answer:

The given quadratic equation is √2x² + x + √2 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = √2, b = 1, and c = √2

Therefore, the discriminant of the given equation is

D = b² – 4ac = 1² – 4 x √2 x √2 = 1 – 8 = –7 

Therefore, the required solutions are

Answer 3

30. Solve the equation √3x² - √2x + 3√3 = 0

Answer:

The given quadratic equation is √3x² - √2x + 3√3 = 0

On comparing the given equation with ax² + bx + c = 0, 

we obtain 

a = √3, b = −√2 and c = 3√3

Therefore, the discriminant of the given equation is 

D = b² – 4ac = (-√2)² - 4(√3) (3√3) 

= 2 - 36

= -34

Therefore, the required solutions are

31. Solve the equation \(x^2 + x+\frac1{\sqrt2}=0\)

Answer:

The given quadratic equation is \(x^2 + x+\frac1{\sqrt2}=0\) 

This equation can also be written as √2x² + √2x +1 = 0

On comparing this equation with ax² + bx + c = 0, we obtain

a = √2, b = √2 and c = 1

\(\therefore \) Discriminant (D) = b² - 4ac = (√2)² - 4 x (√2) x 1 = 2 - 4√2

Therefore, the required solutions are

32. Solve the equation \(x^2 + \frac x{\sqrt2}+1=0\)

Answer:

The given quadratic equation is \(x^2 + \frac x{\sqrt2}+1=0\)

This equation can also be written as √2x² + x + √2 = 0

On comparing this equation with ax² + bx + c = 0, we obtain

a = √2, b = 1  and c = √2

 \(\therefore \) Discriminant (D) = b² - 4ac = 1² - 4 x √2 x √2 = 1-8 = -7

Therefore, the required solutions are

33. Evaluate:

\(\left[i^{18}+\left(\frac 1i\right)^{25}\right]^3\)

Answer:

34. For any two complex numbers z₁ and z₂, prove that 

Re (z₁z₂) = Re z₁ Re z₂ – Im z₁ Im z₂

Answer:

Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂

⇒ Re (z₁z₂) = x₁x₂ - y₁y₂

⇒ Re (z₁z₂) = Re z₁ Re z₂ - Im z, Im z₂

Hence, proved.

35. Reduce \((\frac1{1-4i}-\frac2{1+i})(\frac{3-4i}{5+i})\) to the standard form.

Answer:

This is the required standard form.

36. If x – iy = \(\sqrt{\frac{a-ib}{c-id}}\) prove that (x² + y²)² = \(\frac{a^2+b^2}{c^2+d^2}\)

Answer:

x – iy = \(\sqrt{\frac{a-ib}{c-id}}\) 

On comparing real and imaginary parts, we obtain

Hence, proved.

37. Convert the following in the polar form:

 (i) \(\frac{1+7i}{(2-1)^2}\)

 (ii) \(\frac{1+3i}{1-2i}\)    

Answer:

(i) Here,

z = \(\frac{1+7i}{(2-1)^2}\)

 

Let r cos θ = –1 and r sin θ = 1 

On squaring and adding, we obtain 

r² (cos² θ + sin² θ) = 1 + 1

⇒ r² (cos² θ + sin² θ) = 2 

⇒ r² = 2 [cos² θ + sin² θ = 1]

⇒ r = √2     [Conventionally, r > 0]

\(\therefore\) √2 cosθ = -1 and √2 sinθ = 1

⇒ cosθ = \(\frac{-1}{\sqrt2}\) and sinθ = \(\frac{-1}{\sqrt2}\)

\(\therefore\) θ = \(\pi-\frac{\pi}4=\frac{3\pi}{4}\)    [As θ lies in II quadrant]

∴z = r cosθ + i r sinθ

This is the required polar form.

(ii) Here,

z = \(\frac{1+3i}{1-2i}\)

Let r cos θ = –1 and r sin θ = 1 

On squaring and adding, 

we obtain r² (cos²θ + sin²θ)

= 1 + 1 

⇒ r² (cos²θ + sin²θ) = 2 

⇒ r² = 2 [cos²θ + sin²θ = 1]

\(\therefore\) z = r cos θ + i r sin θ

This is the required polar form.

Answer 4

38. Solve the equation 3x² - 4x + \(\frac{20}3\) = 0

Answer:

The given quadratic equation is 3x² - 4x + \(\frac{20}3\) = 0

This equation can also be written as 9x² - 12x + 20 = 0

On comparing this equation with ax² + bx + c = 0, 

we obtain a = 9, b = –12, and c = 20

Therefore, the discriminant of the given equation is 

D = b² – 4ac = (–12)² – 4 × 9 × 20 = 144 – 720 = –576 

Therefore, the required solutions are

39. Solve the equation x² - 2x + \(\frac32\) = 0

Answer:

The given quadratic equation is x² - 2x + \(\frac32\) = 0

This equation can also be written as 2x² - 4x + 3 = 0

On comparing this equation with ax² + bx + c = 0, 

we obtain a = 2, b = –4, and c = 3

Therefore, the discriminant of the given equation is 

D = b² – 4ac = (–4)² – 4 × 2 × 3 = 16 – 24 = –8

Therefore, the required solutions are

40. Solve the equation 27x² – 10x + 1 = 0

Answer:

The given quadratic equation is 27x² – 10x + 1 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 27, b = –10, and c = 1 

Therefore, the discriminant of the given equation is 

D = b² – 4ac = (–10)² – 4 × 27 × 1 = 100 – 108 = –8

Therefore, the required solutions are

41. Solve the equation 21x² – 28x + 10 = 0

Answer:

The given quadratic equation is 21x² – 28x + 10 = 0 

On comparing the given equation with ax² + bx + c = 0, 

we obtain a = 21, b = –28, and c = 10

Therefore, the discriminant of the given equation is 

D = b² – 4ac = (–28)² – 4 × 21 × 10 = 784 – 840 = –56 

Therefore, the required solutions are

42. If, z₁ = 2 - i, z₂ = 1 + i, find \(\left|\frac{z_1+z_2+1}{z_1 -z_2+1}\right|\) 

Answer:

z₁ = 2 - i, z₂ = 1 + i

Thus, the value of \(\left|\frac{z_1+z_2+1}{z_1 -z_2+1}\right|\) is √2.

43. If a + ib = \(\frac{(x+i)^2}{2x^2+1}\), prove that a² + b² = \(\frac{(x+i)^2}{(2x+1)^2}\) 

Answer:

On comparing real and imaginary parts, we obtain

Hence, proved.

44. Let z₁ = 2 - i, z₂ = -2 + i. Find

(i) \(Re\left(\frac{z_1z_2}{\overline{z_1}}\right)\)

(ii) \(Im\left(\frac{1}{z_1\overline{z}_1}\right)\)

Answer:

z₁ = 2 - i, z₂ = -2 + i

(i) z₁z₂ = (2 - i)(-2 + i) = -4 + 2i + 2i - i² = -4 + 4i -(-1) = -3 + 4i

On multiplying numerator and denominator by (2 – i), we obtain

On comparing real parts, we obtain

\(Re\left(\frac{z_1z_2}{\overline{z_1}}\right)\) = \(\frac{-2}5\) 

(ii) \(\frac{1}{z_1\bar{z}_1} = \frac{1}{(2-i)(2+i)}=\frac{1}{(2)^2+(1)^2}=\frac15\) 

On comparing imaginary parts, we obtain

\(Im\left(\frac{1}{z_1\overline{z}_1}\right)\) = 0

45. Find the modulus and argument of the complex number \(\frac{1+2i}{1-3i}\) 

Answer:

Let z = \(\frac{1+2i}{1-3i}\) , then

On squaring and adding, we obtain

Therefore, the modulus and argument of the given complex number are \(\frac{1}{\sqrt2}\) and \(\frac{3\pi}{4}\) respectively.

46. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i.

Answer:

Let z = (x – iy) (3 + 5i)

It is given that, 

\(\bar z=-6-24i\)

\(\therefore\) (3x + 5y) - i(5x - 3y) = -6 - 24i

Equating real and imaginary parts, we obtain

3x + 5y = -6       ......(i)

5x - 3y = 24        ......(ii)

Multiplying equation (i) by 3 and equation (ii) by 5 and then adding them, we obtain

Putting the value of x in equation (i), we obtain

Thus, the values of x and y are 3 and –3 respectively.

49. Find the modulus of \(\frac{1+i}{1-i}-\frac{1-i}{1+i}\) .

Answer:

Answer 5

50. If (x + iy)³ = u + iv, then show that: \(\frac ux+\frac v y= 4(x^2-y^2)\) 

Answer:

(x + iy)² = u + iv

On equating real and imaginary parts, we obtain

Hence, proved.

51. If α and β are different complex numbers with |β| = 1, then find \(\left|\frac{\beta-\alpha}{1-\alpha\beta}\right|\)

Answer:

Let α = a + ib and β = x + iy 

It is given that, |β| = 1

\(\therefore\sqrt{x^2+y^2}=1\)

⇒ x² + y² = 1    ........(i)

= 1

\(\therefore\) \(\left|\frac{\beta-\alpha}{1-\alpha\beta}\right|\) = 1

52. Find the number of non-zero integral solutions of the equation |1 - i|^x = 2^x

Answer:

|1 - i|^x = 2^x

Thus, 0 is the only integral solution of the given equation. Therefore, the number of nonzero integral solutions of the given equation is 0.

53. If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that: 

(a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B².

Answer:

(a + ib) (c + id) (e + if) (g + ih) = A + iB

On squaring both sides, we obtain 

(a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B². Hence proved.

54. If \(\left(\frac{1+i}{1-i}\right)^m\) then find the least positive integral value of m.

Answer:

\(\therefore\) m = 4k, where k is some integer.

Therefore, the least positive integer is 1. 

Thus, the least positive integral value of m is 4 (= 4 × 1).