Question

NCERT Solutions Class 11 Maths Chapter 8 Binomial Theorem is the best study material for preparation for tough exams like JEE Mains, JEE Advance, NTSE, and Olympiad. NCERT Solutions are explained in layman's language.

This NCERT Solution Class 11 is packed with answers to all kinds of questions.

• History of binomial theorem – binomial theorem was first introduced by Euclid in the 4^th century BC. Euclid was a Greek mathematician. He also brought forward the binomial theorem with the exponent of 2. It was also found that cubes of binomial theorem were known to the people in the 6^th century AD in India. The very first introduction of the combination method is mentioned in “chandahsastra” given by Pingala in 200 BC. In the 10^th century AD, Halayudha describes the binomial theorem in a unique form which is today known as Pascal’s triangle.

• Statement and proof of the binomial theorem for positive integral indices – the binomial theorem states that the total number of terms present in the expansion of the binomial theorem is more than that of the index. In the expansion of (a+b)^n, the number of terms is n+1. Where n be any positive integer.
• Properties of Binomial Theorem – we notice the power of a and b where the power of a is decreasing by 1 in successive order while the power of b is increasing by 1 in the same way. For example: (a+b)³ = a³ + 3a²b +3ab² + b³. Here in the very first term, the a³ exponent of a is 3 and an exponent of b is 0. In second term 3a²b we have an exponent of a is 2 while the exponent of b is 1. For third term 3ab², we have an exponent of an equal to 1 and that of b is 2. Then in the last term b³, the exponent of a is 0 while the exponent of b is 3.

• Pascal’s triangle – Pascal’s triangle is a triangular array of the coefficient of the binomial expansion.

Our experts advise us to refer to our NCERT Solutions Class 11 Maths to ace their boards and competitive exams.

Answer 1

NCERT Solutions Class 11 Maths Chapter 8 Binomial Theorem

1. Expand the expression (1– 2x)⁵

Answer:

By using Binomial Theorem, the expression (1– 2x)⁵ can be expanded as

(1– 2x)⁵

2. Expand the expression \(\left(\frac2x-\frac x2\right)^5\)

Answer:

By using Binomial Theorem, the expression \(\left(\frac2x-\frac x2\right)^5\) can be expanded as

\(\left(\frac2x-\frac x2\right)^5\)

3. Expand the expression (2x – 3)⁶

Answer:

By using Binomial Theorem, the expression (2x – 3)⁶ can be expanded as

(2x – 3)⁶

4. Expand the expression \(\left(\frac x3+\frac1x\right)^5\) 

Answer:

By using Binomial Theorem, the expression \(\left(\frac x3+\frac1x\right)^5\) can be expanded as

\(\left(\frac x3+\frac1x\right)^5\)

5. Expand \(\left(x+\frac1x\right)^6\) 

Answer:

By using Binomial Theorem, the expression \(\left(x+\frac1x\right)^6\) can be expanded as

\(\left(x+\frac1x\right)^6\) 

6. Using Binomial Theorem, evaluate (96)³

Answer:

96 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, binomial theorem can be applied. 

It can be written that, 96 = 100 – 4

7. Using Binomial Theorem, evaluate (102)⁵

Answer:

102 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied. 

It can be written that, 102 = 100 + 2

∴ (102)⁵ = (100 + 2)⁵

8. Using Binomial Theorem, evaluate (101)⁴

Answer:

101 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied. 

It can be written that, 101 = 100 + 1

∴ (101)⁴ = (100 + 1)⁴

9. Using Binomial Theorem, evaluate (99)⁵

Answer:

99 can be written as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied. 

It can be written that, 99 = 100 – 1

∴ (99)⁵ = (100 - 1)⁵

10. Using Binomial Theorem, indicate which number is larger (1.1)¹⁰⁰⁰⁰ or 1000.

Answer:

By splitting 1.1 and then applying Binomial Theorem, the first few terms of (1.1)¹⁰⁰⁰⁰ can be obtained as

(1.1)¹⁰⁰⁰⁰ = (1 + 0.1)¹⁰⁰⁰⁰

Hence, (1.1)¹⁰⁰⁰⁰ > 1000

11. Find (a + b)⁴ – (a – b)⁴ . Hence, evaluate.

 \((\sqrt3+\sqrt2)^4-(\sqrt3-\sqrt2)^4\) 

Answer:

Using Binomial Theorem, the expressions, (a + b)⁴ and (a – b)⁴ , can be expanded as

By putting a = √3 and b = √2, we obtain

12. Find (x + 1)⁶ + (x – 1)⁶ . Hence or otherwise evaluate.

\((\sqrt2+1)^6+(\sqrt2-1)^6\) 

Answer:

Using Binomial Theorem, the expressions, (x + 1)⁶ and (x – 1)⁶ , can be expanded as

By putting x = \(\sqrt2\), we obtain

13. Show that 9ⁿ⁺¹ - 8n - 9 is divisible by 64, whenever n is a positive integer.

Answer:

In order to show that 9ⁿ⁺¹ - 8n - 9 is divisible by 64, it has to be proved that,

9ⁿ⁺¹ - 8n - 9 = 64k , where k is some natural number 

By Binomial Theorem,

For a = 8 and m = n + 1, we obtain

is a natural number

Thus, 9ⁿ⁺¹ - 8n - 9 is divisible by 64, whenever n is a positive integer.

14. Prove that.

 \(\displaystyle\sum_{r =0}^n3^r\,^nC_r=4^n\) 

Answer:

By Binomial Theorem,

By putting b = 3 and a = 1 in the above equation, we obtain

Hence, proved.

Answer 2

15. Find the coefficient of x⁵ in (x + 3)⁸

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\)

Assuming that x⁵ occurs in the (r + 1)^th term of the expansion (x + 3)⁸ , we obtain

T_r+1 = \(^8C_r(x)^{8-r}(3)^r\) 

Comparing the indices of x in x⁵ and in T_{r +1}, 

we obtain r = 3 

Thus, the coefficient of x⁵ is 

16. Find the coefficient of a⁵b⁷ in (a – 2b)¹²

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b) n is given by

T_r+1 = \(^nC_ra^{n-r}b^r\)

Assuming that a⁵b⁷ occurs in the (r + 1)^th term of the expansion (a – 2b)¹², we obtain

Comparing the indices of a and b in a⁵ b⁷ and in T_{r +1}, 

we obtain r = 7 

Thus, the coefficient of a⁵b⁷ is

17. Write the general term in the expansion of (x² – y)⁶

Answer:

It is known that the general term T_r+1 {which is the (r + 1)^th term} in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Thus, the general term in the expansion of (x² – y⁶) is

18. Write the general term in the expansion of (x² – yx)¹² , x ≠ 0

Answer:

It is known that the general term T_r+1 {which is the (r + 1)^th term} in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) . 

Thus, the general term in the expansion of(x² – yx)¹² is

19. Find the 4th term in the expansion of (x – 2y)¹².

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Thus, the 4^th term in the expansion of (x – 2y)¹² is

20. Find the 13^th term in the expansion of \(\left(9x - \frac1{3\sqrt x}\right)^{18},x \ne0\)

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Thus, 13^th term in the expansion of  \(\left(9x - \frac1{3\sqrt x}\right)^{18}\) is '

21. Find the middle terms in the expansions of \(\left(3-\frac{x^3}{6}\right)^7\)

Answer:

It is known that in the expansion of (a + b)ⁿ , if n is odd, then there are two middle terms,

namely \(\left(\frac{n+1}2\right)^{th}\) term and \(\left(\frac{n+1}2+1\right)^{th}\) term.

Therefore, the middle terms in the expansion \(\left(3-\frac{x^3}{6}\right)^7\) are \(\left(\frac{7+1}2\right)^{th}\) term and \(\left(\frac{7+1}2+1\right)^{th}=5^{th}\) term

Thus, the middle terms in the expansion of \(\left(3-\frac{x^3}{6}\right)^7\) are \(-\frac{105}{8}x^9\) and \(\frac{35}{48}x^{12}\) .

22. Find the middle terms in the expansions of \(\left(\frac x3 + 9y \right)^{10}\) 

Answer:

It is known that in the expansion (a + b) n , if n is even, then the middle term is \(\left(\frac{n}2+1\right)^{th}\) term.

Therefore, the middle term in the expansion of \(\left(\frac x3 + 9y \right)^{10}\) is \(\left(\frac{10}2+1\right)^{th}\) = 6^th

Thus, the middle term in the expansion of \(\left(\frac x3 + 9y \right)^{10}\) is 61236 x⁵ y⁵ .

23. In the expansion of (1 + a)^{m + n} , prove that coefficients of a^m and aⁿ are equal.

Answer:

It is known that (r + 1)^th term, (T^r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Assuming that a^m occurs in the (r + 1)^th term of the expansion (1 + a)^{m + n}, we obtain

Comparing the indices of a in a^m and in T_{r + 1}, 

we obtain

r = m 

Therefore, the coefficient of a^m is

Assuming that aⁿ occurs in the (k + 1)^th term of the expansion (1 + a)^m+n , we obtain

Comparing the indices of a in aⁿ and in T_{k + 1}, 

we obtain k = n 

Therefore, the coefficient of aⁿ is

Thus, from (1) and (2), it can be observed that the coefficients of a^m and aⁿ in the expansion of (1 + a)^{m + n} are equal.

Answer 3

24. The coefficients of the (r – 1)^th , r^th and (r + 1)^th terms in the expansion of (x + 1)n are in the ratio 1:3:5. Find n and r.

Answer:

It is known that (k + 1)^th term, (T_k+1), in the binomial expansion of (a + b)ⁿ is given by

T_k+1 = \(^nC_ra^{n-k}b^k\) .

Therefore, (r – 1)^th term in the expansion of (x + 1)ⁿ is

(r + 1) term in the expansion of (x + 1)ⁿ is

r^th term in the expansion of (x + 1)ⁿ is

Therefore, the coefficients of the (r – 1)^th , r^th, and (r + 1)^th terms in the expansion of (x + 1)ⁿ \(^nC_{r-2},\,^nC_{r-1}\) and \(^nC_r\) are respectively. Since these coefficients are in the ratio 1:3:5, we obtain

Multiplying (1) by 3 and subtracting it from (2), we obtain 

4r – 12 = 0 

⇒ r = 3 

Putting the value of r in (1), we obtain 

n – 12 + 5 = 0 

⇒ n = 7 

Thus, n = 7 and r = 3

25. Prove that the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is twice the coefficient of xⁿ in the expansion of (1 + x)^2n–1.

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Assuming that xⁿ occurs in the (r + 1)^th term of the expansion of (1 + x)²ⁿ , we obtain

Comparing the indices of x in xⁿ and in T_{r + 1}, we obtain r = n 

Therefore, the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is

Assuming that xⁿ occurs in the (k +1)^th term of the expansion (1 + x)^{2n – 1} , we obtain

From (1) and (2), it is observed that

Therefore, 

the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is twice the coefficient of xⁿ in the expansion of (1 + x)/^2n–1 . 

Hence, proved.

26. Find a positive value of m for which the coefficient of x 2 in the expansion (1 + x) m is 6.

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Assuming that x² occurs in the (r + 1)^th term of the expansion (1 +x)^m, we obtain

Comparing the indices of x in x² and in T_{r + 1}, we obtain r = 2 

Therefore, the coefficient of x² is \(^mC_2\)

It is given that the coefficient of x² in the expansion (1 + x)^m is 6.

Thus, the positive value of m, for which the coefficient of x² in the expansion (1 + x)^m is 6, is 4.

27. Find a, b and n in the expansion of (a + b)ⁿ if the first three terms of the expansion are 729, 7290 and 30375, respectively.

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

The first three terms of the expansion are given as 729, 7290, and 30375 respectively. 

Therefore, we obtain

Dividing (2) by (1), we obtain

Dividing (3) by (2), we obtain

From (4) and (5), we obtain

Substituting n = 6 in equation (1), we obtain a⁶ 

= 729

⇒ a = \(\sqrt[6]{729}\) = 3

From (5), we obtain

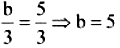
Thus, a = 3, b = 5, and n = 6.

28. Find a if the coefficients of x² and x³ in the expansion of (3 + ax)⁹ are equal.

Answer:

It is known that (r + 1)^th term, (T_r+1), in the binomial expansion of (a + b)ⁿ is given by

T_r+1 = \(^nC_ra^{n-r}b^r\) .

Assuming that x² occurs in the (r + 1)^th term in the expansion of (3 + ax)⁹ , we obtain

Comparing the indices of x in x² and in T_{r + 1}, we obtain 

r = 2 

Thus, the coefficient of x² is

Assuming that x³ occurs in the (k + 1)^th term in the expansion of (3 + ax)⁹ , we obtain

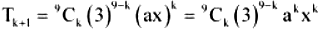
Comparing the indices of x in x³ and in T_{k+ 1}, we obtain k = 3 

Thus, the coefficient of x³ is

It is given that the coefficients of x² and x³ are the same.

Thus, the required value of a is 9/7.

29. Find the coefficient of x⁵ in the product (1 + 2x)⁶ (1 – x)⁷ using binomial theorem.

Answer:

Using Binomial Theorem, the expressions, (1 + 2x)⁶ and (1 – x)⁷ , can be expanded as

The complete multiplication of the two brackets is not required to be carried out. 

Only those terms, which involve x⁵ , are required. 

The terms containing x⁵ are 

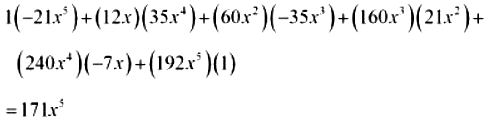
Thus, the coefficient of x⁵ in the given product is 171.

Answer 4

30. If a and b are distinct integers, prove that a – b is a factor of aⁿ – bⁿ , whenever n is a positive integer. [write aⁿ = (a – b + b)ⁿ and expand]

Answer:

In order to prove that (a – b) is a factor of (aⁿ – bⁿ), it has to be proved that aⁿ – bⁿ = k (a – b), where k is some natural number 

It can be written that, a = a – b + b

This shows that (a – b) is a factor of (aⁿ – bⁿ), where n is a positive integer.

31. Evaluate.

\((\sqrt3+\sqrt2)^6-(\sqrt3-\sqrt2)^6\)

Answer:

Firstly, the expression (a + b)⁶ – (a – b)⁶ is simplified by using Binomial Theorem. This can be done as

Putting a = √3 and b = √2, we obtain 

32. Find the value of \((a^2 + \sqrt{a^2-1})^4+(a^2-\sqrt{a^2-1})^4\)

Answer:

Firstly, the expression (x + y)⁴ + (x – y)⁴ is simplified by using Binomial Theorem. This can be done as

Putting x = a² and y = \(\sqrt{a^2-1}\) , we obtain

33. Find an approximation of (0.99)⁵ using the first three terms of its expansion.

Answer:

0.99 = 1 – 0.01

\(\therefore\) (0.99)⁵ = (1 - 0.01)⁵

Thus, the value of (0.99)⁵ is approximately 0.951.

34. Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of \(\left({\sqrt[4]{2}}+\frac{1}{\sqrt[4]{3}}\right)\) is √6 : 1

Answer:

In the expansion,

Fifth term from the beginning = \(^nC_4a^{n-4}b^4\)

Fifth term from the end = \(^nC_4a^4b^{n-4}\)

Therefore, it is evident that in the expansion of \(\left(\sqrt[4]{2}+\frac1{\sqrt[4]{3}}\right)\) the fifth term from the beginning is \(^nC_4(\sqrt[4]2)^{n-4}\left(\frac{1}{\sqrt[4]3}\right)^4\)

and the fifth term from the end is \(^nC_{n-4}(\sqrt[4]2)^{4}\left(\frac{1}{\sqrt[4]3}\right)^{n-4}\)

It is given that the ratio of the fifth term from the beginning to the fifth term from the end is √6 : 1. 

Therefore, from (1) and (2), we obtain

Thus, the value of n is 10.

35. Expand using Binomial Theorem \(\left(1+\frac x2-\frac2x\right)^4,x\ne0\) 

Answer:

Using Binomial Theorem, the given expression \(\left(1+\frac x2-\frac2x\right)^4\) can be expanded as 

Again by using Binomial Theorem, we obtain

From (1), (2), and (3), we obtain

36. Find the expansion of (3x² - 2ax + 3a²)³ using binomial theorem.

Answer:

Using Binomial Theorem, the given expression (3x² - 2ax + 3a²)³ can be expanded as

Again by using Binomial Theorem, we obtain

From (1) and (2), we obtain