Question

A particular one-dimensional potential well has the following bound-state single-particle energy eigenfunctions:

\(\psi_a(x), \psi_b(x), \psi_c(x)...., \) where \(E_a < E_b< E_c ....\)

Two non-interacting particles are placed in the well. For each of the cases (a), (b), (c) listed below write down:

The two lowest total energies available to the two-particle system, the degeneracy of each of the two energy levels, the possible two-particle wave functions associated with each of the levels.

(Use \(\psi\) to express the spatial part and a ket \(|S,m_s\rangle\) to express the spin part. S is the total spin.) 

(a) Two distinguishable spin-1/2 particles.

(b) Two identical spin-1/2 particles.

(c) Two identical spin-0 particles.

Answer 1

As the two particles, each of mass M, have no mutual interaction, their spatial wave functions separately satisfy the Schrodinger equation:

The equations may also be combined to give

Consider the two lowest energy levels (i) and (ii).

(a) Two distinguishable spin-1/2 particles.

(i) Total energy = E_a + E_a, degeneracy = 4. The wave functions are

(ii) Total energy = E_a + E_b, degeneracy = 8. The wave functions are

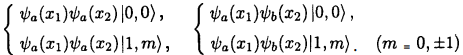
(b) Two identical spin-1/2 particles.

(i) total energy = E_a + E_b, degeneracy = 1. The wave function is

\(\psi_a(x_1)\psi_a(x_2)|0,0\rangle\).

(ii) total energy = E_a + E_b, degeneracy = 4. The wave functions are

(c) Two identical spin-0 particles.

(i) Total energy = E_a + E_b, degeneracy = 1. The wave function is

\(\psi_a(x_1)\psi_a(x_2)|0,0\rangle\).

(ii) Total energy = E_a + E_b, degeneracy = 1. The wave function is