а§≤а•За§Ва§Є ৮ড়а§∞а•Нুৌ১ৌ а§Єа•В১а•На§∞ ৵а•На§ѓа•Б১а•Н৙১а•Н১ড়
ুৌ৮а•Нৃ১ৌа§Уа§В
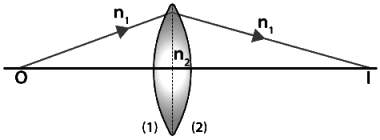
а§≤а•За§Ва§Є ৮ড়а§∞а•Нুৌ১ৌ а§Єа•В১а•На§∞ а§Ха•А ৵а•На§ѓа•Б১а•Н৙১а•Н১ড় а§Ха•З а§≤а§ња§П ৮ড়ুа•Н৮а§≤а§ња§Цড়১ а§Іа§Ња§∞а§£а§Ња§Па§Б а§≤а•А а§Ча§И а§єа•Иа§Ва•§
- а§Жа§За§П а§К৙а§∞ а§Ха•А а§Ы৵ড় а§Ѓа•За§В ৶ড়а§Ца§Ња§П а§Ча§П ৙১а§≤а•З а§≤а•За§Ва§Є ৙а§∞ ৵ড়а§Ъа§Ња§∞ а§Ха§∞а•За§В а§Ьа§ња§Єа§Ѓа•За§В ৶а•Л а§Е৙৵а§∞а•Н১а§Х ৪১৺а•За§В а§єа•Иа§В а§Ьড়৮а§Ха•А ৵а§Ха•На§∞১ৌ ১а•На§∞а§ња§Ьа•На§ѓа§Ња§Па§Б а§Ха•На§∞ু৴а§Г R1 а§Фа§∞ R2 а§єа•Иа§Ва•§
- ুৌ৮ৌ а§Ха§њ а§Ж৪৙ৌ৪ а§Ха•З а§Ѓа§Ња§Іа•На§ѓа§Ѓ а§Фа§∞ а§≤а•За§Ва§Є а§Єа§Ња§Ѓа§Ча•На§∞а•А а§Ха§Њ а§Е৙৵а§∞а•Н১৮ৌа§Ва§Х а§Ха•На§∞ু৴а§Г n1 а§Фа§∞ n2 а§єа•Иа•§
৵а•На§ѓа•Б১а•Н৙১а•Н১ড়
а§≤а•За§Ва§Є ৮ড়а§∞а•Нুৌ১ৌ а§Єа•В১а•На§∞ а§Ха•А а§Єа§В৙а•Ва§∞а•На§£ ৵а•На§ѓа•Б১а•Н৙১а•Н১ড় ৮а•Аа§Ъа•З ৵а§∞а•На§£а§ња§§ а§єа•Иа•§ а§Па§Ха§≤ а§Ча•Ла§≤а§Ња§Ха§Ња§∞ ৪১৺ ৙а§∞ а§Е৙৵а§∞а•Н১৮ а§Ха•З а§Єа•В১а•На§∞ а§Ха§Њ а§Й৙ৃа•Ла§Ч а§Ха§∞а§Ха•З, а§єа§Ѓ а§Ха§є а§Єа§Х১а•З а§єа•Иа§В а§Ха§њ,
৙৺а§≤а•А ৪১৺ а§Ха•З а§≤а§ња§П,
\(\frac{n_2}{v_1}-\frac{n_1}{u}=\frac{n_2-n_1}{R_1}\quad \ldots(1)\)
৶а•Ва§Єа§∞а•А ৪১৺ а§Ха•З а§≤а§ња§П,
\(\frac{n_1}{v}-\frac{n_2}{v_1}=\frac{n_1-n_2}{R_2} \quad\ldots(2)\)
а§Еа§ђ а§Єа§Ѓа•Аа§Ха§∞а§£ (1) а§Фа§∞ (2) а§Ьа•Лৰ৊৮а•З ৙а§∞,
\(\frac{n_1}{v}-\frac{n_1}{u}=\left(n_2-n_1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right] \)
\( \Rightarrow \frac{1}{v}-\frac{1}{u}=\left(\frac{n_2}{n_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
а§Ьа§ђ u = вИЮ а§Фа§∞ v = f
\(\frac{1}{f}=\left(\frac{n_2}{n_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
а§≤а•За§Хড়৮,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
а§Е১: а§єа§Ѓ а§ѓа§є а§Ха§є а§Єа§Х১а•З а§єа•Иа§В а§Ха§њ,
\(\frac{1}{f}=(\mu-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
а§Ьа§єа§Ња§Б ќЉ ৙৶ৌа§∞а•Н৕ а§Ха§Њ а§Е৙৵а§∞а•Н১৮ৌа§Ва§Х а§єа•Иа•§