Huygens’ Principle
It is based on the following two assumptions:
(1) All the particles on a given wavefront (Called primary wavefront) can be regarded as point sources of new disturbance called the secondary wavelets which travel out with the same velocity as that of the original waves, provided the medium is the same.
(2) A surface tangential to the secondary wavelets gives the position and shape of the new wavefront.
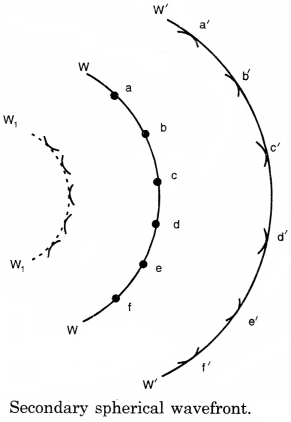
Illustration. Consider O to be a point source of light and WW a spherical wavefront originating from it Fig. (a) All the points a, b, c,... on this will be vibrating in unison and may be regarded as sources of secondary disturbances. To find the position of the wavefront after an interval t second, draw spheres of radius ct (where c is the velocity of light) with a, b, c,... as centre which wall be Huygens' secondary waves. These waves touch a sphere W'W' whose centre is at O. The spherical surface constitutes the new secondary wavefront which is also spherical.
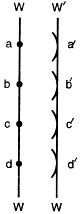
If the source of light is at a large distance, we will have a plane wavefront as shown in Fig. (b).
Referring again to Fig. (a), it will be seen that the secondary wavelets spread out in the backward direction also, and W1W1 represents the envelope of these back portions of the waves by dotted lines. Thus W1W1 is also a secondary wavefront which in reality does not exist. To account for this difficulty, it is assumed that the only effective part of the secondary wavelets is the portion which lies on the forward secondary wavefront. The remaining part of the secondary wavelet is ineffective. Thus, there are no back waves and the wavefront W1W1 is absent.
(a) Let XY be a plane refracting surface separating rarer medium I of refractive index µ1, from denser medium II of refractive index µ2 [µ2 > µ1], then
\(\frac{\mu_2}{\mu_1} = 1\mu_2 = \frac{v_1}{v_2}\)
Where v1 is the velocity of light in medium I and v2 is the velocity of light in medium II.
According to Huygens’ principle, every point on incident wavefront AB is a source of secondary wavelets. By the time wavelet from point B reaches at point C, the wavelet from point A would have reached at point D s.t. time taken from B to C is equal to time taken from A to D.
i.e. t = \(\frac{BC}{v_1} = \frac{AD}{v_2}\)
\(\frac{BC}{AD} = \frac{v_1}{v_2}\) ..........(i)
First law of refraction

This is first law of refraction and is called Snell’s law.
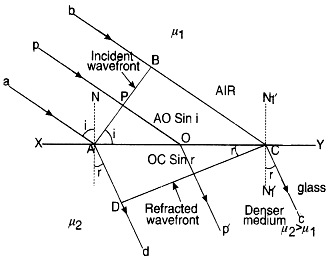
Second law of refraction: Since incident ray, refracted ray and the normal, all lie on the same plane XY at the point of incidence. This proves second law of refraction.
(b) Behaviour of wavefront while passing through:
(i) Prism
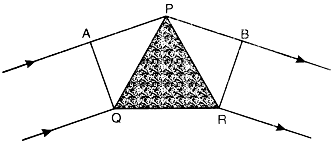
Consider a small angled prism PQR and a plane wavefront AQ incident on the prism. The course of rays is as shown is Fig. (b). According to Huygens’ principle, every point on wavefront AQ is the source of secondary wavelets. The secondary wavelets from Q travel through the material of the prism and the secondary wavelets from A travel almost in air, and the other wavelets travel different thicknesses of the glass prism. Since the speed of light in glass is less than the speed of light in air thus the ray of light bends towards the base after passing through the prism.

(ii) Lens
Consider a convex lens XY as shown in Fig. (c) and a plane wavefront AB incident on it. The course of rays is as shown in the figure. According to Huygens’ principle, every point on wavefront AB is the source of secondary wavelets. The secondary wavelets from A or B travel almost through air and the secondary wavelets from C travel a distance P1P2 almost inside the material of the lens. Since speed of fight in glass is less than the speed of fight in air. Thus the rays of fight takes the form of spherical wave form DP2F.