Question

Inverse of a Matrix by Elementary Operations

Answer 1

Let X, A and B be matrices of the same order such that X = AB. In order to apply a sequence of elementary row operations on the matrix equation X = AB,we will apply these row operations simultaneously on X and on the first matrix A of the product AB on RHS.

Similarly, in order to apply a sequence of elementary column operations on the matrix equation X=AB, we will apply, these operations simultaneously on X and on the second matrix B of the product AB on R.H.S

In view of the above discussion, we canclude that if A is a matrix such that A^-1 exists, then to find A^-1 using elementary row operations, write A = IA and apply a sequence of row operation on A = IA till we get, I = BA. The matrix B will be the inverse of A. Similarly, if we wish to find A^-1 using column oprations, then write A = A I and apply a sequence of column of operations on A = A I till we get, I = AB.

Remark:

In case, after applying one or more elementary row (column) operations on A = IA (A = AI), if we obtain all zeros in one or more rows of the matrix A on L.H.S., then A^-1 does not exist.

→ A matrix is an ordered rectangular arrray of numbers (may be real or complex) or functions.

→ Elements or entries of the mattrix are the numbers or functions in the array.

→ Rows of matrix are the horizontal lines of elements.

→ Columns of matrix are the vertical lines of elements.

Order of a Matrix:

If a matrix has "m" rows and "n" columns, then order of the matrix is m × n.

The total numbers of elements in the matrix of m × n will be mn.

Any point (x, y) in a plane can be represented in the matrix format as below :

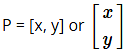
 Types of a Matrix

→Column Matrix

• A matrix having only one column and any number of rows.
• General Form: A = [a_ij]_m×1, order of the matrix is m × 1.

→ Row Matrix

• A matrix having only one row and any number of columns.
• General Form = A = [a_ij]_1×n order of the matrix is 1 × n.

→ Square Matrix

• A matrix of order m × n, such that m = n
• General Form = A = [a_ij]_m×m, order of the matrix is m.

→ Diagonal Matrix

• A square matrix is said to be a diagonal matrix, if all its non-diagonal elements zero.
• General = A = [b_ij]_m×m, order of the matrix is m where b_ij = 0, if i = j;

→ Scalar Matrix

• A diagonal matrix is said to be a scalar matrix if its diagonal elements are equal.
• General Form = A = [b_ij]_m×m, order of the matrix is m where b_ij = 0, if i ≠ j and b_ij = 1, if i = j

→ Zero Matrix

A matrix is said to be zero matrix or null matrix if all its elements are zero and is denoted by O.

→ Equal Matrices

Two matrices are said to be equal if:

• they are of the same order
• each element of A is equal to the corresponding element of B.

→ Operation on Matrices

Addition of Matrices

• The sum of matrices A + B is defined only if matrices A and B are of same order.
• If A = [a_ij]_m×n and B = [b_ij]_m×n then, A + B = [a_ij + b_ij]_m×n

→ Properties of Addition of Matrices

Let A = [a_ij], B = [b_ij] and C = [c_ij] are three matrices of order m × n.

Commutative Law

A + B = B + A

Associative Law

(A+ B) + C = A + (B + C)

Existence of Additive Identity

A zero matrix (O) of order m × n (same as of A), is additive identity, if A + 0 = A = 0 + A

Existence of Additive Inverse

If A is a square matrix, then the matrix (- A) is called additive inverse, if A + (- A) = 0 = (- A) + A

- A is the additive inverse of A or negative of A.

Cancellation Law

A + B = A + C ⇒ B = C (Left cancellation law)

B + A = C + A ⇒ B = C (Right cancellation law)

→Subtraction of Matrices

Let A and B be two matrices of the same order, then subtraction of matrices, A - B, is defined as A - B = [a_ij - b_ij]_m×n, where A = [a_ij]_m×n, B = [b_ij]_m×n.

→ Multiplication of Matrices

Multiplication of a Matrix by a Scalar

Let A = [a_ij]_m×n be a matrix and k be any scalar. Then, the matrix obtained by multiplying each element of A by k is called the scalar multiple of A by k and is denoted by kA, given as kA = [ka_ij]_m×n

→ Properties of Scalar Multiplication :

If A and B are matrices of order m × n, then

• k(A + B) = kA + kB)
• (k₁ + k₂)A = k₁A + k₂A
• k₁k₂A = k₁ (k₂A) = k₂(k₁A)
• (-k) A = - (kA) = k (- A) also called as negative of a matrix.

Multiplication of Two Matrices

If A = [a_ij] of order m × n and B = [b_ij] of order n × p then the product C = [c_ij] will be a matrix of the order m × p.

Note:

• If AB is defined, then BA need not be defined.
• If A, B are respectively m × n, k × 1 matrices, then both AB and BA are defined if and only if n = k and 1 = m.
• If the product of two matrices is a zero matrix, it is not necessary that one of the matrices is a zero matrix.

→ Properties of Multiplication of Matrices

Let A = [a_ij], B = [b_ij] and C = [c_ij] are three matrices of order m x n.

• Commutative Law
  AB ≠ BA
• Associative Law
  (A B) C = A (BC)
• Distributive Law
  • A (B + C) = AB + AC
  • (A + B) C - AC + BC, whenever both sides of equal-ity are defined.

→ Existence of Multiplicative Identity

For every square matrix A, there exists an identity matrix of same order such that IA = AI = A

→ Cancellation Law

If A is non-singular matrix, then

• AB = AC ⇒ B = C (Left cancellation law)
• BA = CA ⇒ B = C (Right cancellation law)
• AB = 0, does not necessarily imply that A = 0 or B = 0 or both A and B = 0

→ Transpose of a Matrix

Let A = [a_ij]_m×n be a matrix of order m × n. Then, the n × m a matrix obtained by interchanging the rows and columns of A is called the transpose of A and is denoted by A' or AT.

→ Properties of Transpose

• (A')' = A
• (A + B)' = A' + B'
• (AB)' = B' A'
• (kA)' = kA'
• (AN)' = (A')N
• (ABC)' = C'B' A'
• A square matrix A = [a_ij] is said to be symmetric if A' = A

Note:

• If A is symmetric then, [a_ij] = [a_ij]
• If A is skew-symmetric then, [a_ij] = - [a_ij]
• All the diagonal elements of a skew-symmetric matrix are zero.

→ Elementary Operation (Transformation) of a Matrix

• There are six operations (transformation) on a matrix, three of which are due to rows and three due to columns.
• Interchanging any two rows (or columns), denoted by R_i ⇔ R_j or C_i ⇔ C_j

→ Invertible Matrices

If A is a square matrix of order m, and if there exists another square matrix B of the same order m, such that AB - BA = I, then B is called the inverse matrix of A and it is denoted by A^-1. In that case A is said to be invertible.