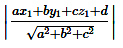Question

Angle Between a Line and a Plane of three dimensional geometry.

Answer 1

Definition : The angle between a line and a plane is the complement of the angle between the line and normal to the plane.

Vector form:

Let equation of line is \(\overrightarrow r = \overrightarrow a + \lambda \overrightarrow b\) and equation of plane is \(\overrightarrow r . \overrightarrow n = d.\) Then the angle 0 between the line and the normal to the plane is

Cartesian form:

Angle between line

→ If a line makes angle α, β and γ with axes OX, OY and OZ respectively. The cosines of these angles are the direction cosines of line, hence, cos α, cos β and cos γ are the direction cosines of the line which is respresented by l, m and n. I = cos α, m = cos β and n = cos γ and cos²α + cos²β + cos²γ = 1

⇒ l² + m² + n² = 1

→ If a line makes angle α, β and γ with axes OX, OY and OZ respectively. The cosines of these angles are the direction cosines of line, hence, cos α, cos β and cos γ are the direction cosines of the line which is respresented by l, m and n. I = cos α, m = cos β and n = cos γ and cos²α + cos²β + cos²γ = 1
⇒ l² + m² + n² = 1
(i) Direction cosines of a line joining two points P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) are :

(ii) The direction ratios of the line segment joining two points P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) are : x₂ - x₁, y₂ - y₁, z₂ - z₁

→ Direction ratios of a line are the numbers which are proportional to the direction cosines of a line. Generally, direction ratios are represented as a, b and c. If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then.

→ The projection of line segment joining the points P(x₁ y₁ z₁) and Q(x₂ y₂ z₂) on a line having direction cosines l, m and n are

|(x₂ - x₁)l + (y₂ - y₁)m + (z₂ - z₁)n|

→ If direction cosines of two lines are l₁ m₁ n₁ and l₂, m₂, n₂ respectively then

cos θ = l₁l₂ + m₁m₂ + n₁n₂

(i) If lines are perpendicular, then

l₁l₂ + m₁m₂ + n₁n₂ = 0

(ii) If lines are parallel, then

\(\frac{l_1}{l_2} = \frac{m_1}{m_2} = \frac{n_1}{n_2}\)

→ If direction cosine of two lines are proportional to a₁, b₁ c₁ and a₂, b₂, c₂ then angle between them

(i) If lines are perpendicular, then

a₁a₂ + b₁b₂ + c₁c₂ = 0

(ii) If lines are parallel, then

\(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)

→ Vector equation of a line that passes through the given point \(\overrightarrow r\) and parallel to a given vector \(\overrightarrow b\) is \(\overrightarrow r = \overrightarrow a + \lambda \overrightarrow b\) where λ, is a non-zero real number.

Answer 2

(i) Cartesian equation of a line through a point (x₁ y₁ z₁) and having direction cosines l, m, n is

\(\frac{x-x_1}{l} = \frac{y-y_1}{m} = \frac{z-z_1}{n}\) (∵ l² + m² + n² = 1)

(ii) If direction ratios of the line is a, b, c then the equation of the line is \(\frac{x-x_1}{a} = \frac{y-y_1}{b} = \frac{z-z_1}{c}\)

→ Equation of a line passing through two points (x₁ y₁ z₁) and (x₂ y₂ z₂) is :

lines, then for acute angle θ

cos θ = |l₁l₂ + m₁m₂ + n₁n₂|

→ Those lines which are neither intersect nor parallel are known as non-coplanar lines. Hence both are on different planes.

→ If L₁ and L₂ be two lines in space then the line segment perpendicular to both the lines are known as shortest distance. If shortest distance line of both lines intersect at point P and Q then PQ is known as shortest distance.

→ Shortest distance between the lines \(\overrightarrow r = \overrightarrow {a_1} + \lambda \overrightarrow {b_1}\) and \(\overrightarrow r = \overrightarrow {a_2} + \mu \overrightarrow {b_2}\) is \(|\frac{​​​​(\overrightarrow {b_1} \times \overrightarrow {b_2}). (\overrightarrow {a_2} \times \overrightarrow {a_1})}{|\overrightarrow {b_1} \times \overrightarrow {b_2}|}|\)

→ The vector equation of a plane which is at a distance d from the origin is \(\overrightarrow r\) n̂ = d, where n̂ is the normal unit vector to the plane through the origin.

• General equation of a plane is ax + by + cz + d = 0
• Normal vector on plane ax + by + cz + d = 0 is \(\overrightarrow x = a \hat i +b \hat j + c \hat k\)
• If l, m, and n be the direction cosines of normal and distance of the plane from the origin is p then normal form of plane is lx + my + nz = d.

→ Cartesian equation of a plane at a distance d from the origin is lx + my + nz = d, where l, m, n are the direction cosines of normal at plane.

→ Equation of the plane which passes through \(\overrightarrow n \text {is} (\overrightarrow r +\overrightarrow a) \overrightarrow n = 0\)

→ Equation of the plane which passes through the point (x₁ y₁ z₁) and having direction cosines A, B, C and perpendicular to the line is :

A(x - x₁) + B(y- y₁) + C(z - z₁) = 0

→ Equation of the plane which passes through three non-collinear points (x₁ y₁ z₁), (x₂ y₂ z₂) and (x₃ y₃ z₃) is :

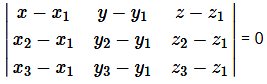
→ Equation of the plane which passes through three non-collinear points \(\overrightarrow a, \overrightarrow b \) and \(\overrightarrow c\) is.

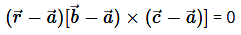
→ Equation of the plane which passes through points (a, 0, 0), (0, b, 0) and (0, 0, c) is :

→ Vector equation of a plane that passes through the intersection of planes d₁ + λ d₂, where λ is any non-zero constant.

→ Vector equation of a plane that passes through the intersection of two given planes A₁x + B₁y + C₁z + D₁ = 0 and A₂ x + B₂y + C₂z + D₂ = 0 is :

(ii) If θ be the angle between the lines →r=→a+λ→br→=a→+λb→ and →r=→xr→=x→ = d, then

→ If θ be the angle between the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0, then

• If planes are mutually perpendicular, then a₁a₂ + b₁b₂ + c₁c₂ = 0
• If planes are parallel, then \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)

→ The distance of a point whose position vector is from the plane is \(\overrightarrow a\) from the plane \(\overrightarrow r \overrightarrow x =d \ is|d-\overrightarrow a \hat x|\)

→ The distance from a point (x₁ y₁ z₁) to the plane ax + by + cz + d = 0 is