Astring is a metal wire whose length is large when compared to its thickness. A stretched string is fixed at both ends, when it is plucked at mid point, two reflected waves of same amplitude and frequency at the ends are travelling in opposite direction and overlap along the length. Then the resultant waves are known as the standing waves (or) stationary waves.
Let two transverse progressive waves of same amplitude a, wave length λ and frequency 'ν', travelling in opposite direction be given by
y1 = a sin(kx – ωt) and y2 = – a sin(kx + ωt)
where ω = 2πν and k = 2π/λ
The resultant wave is given by y = y1 + y2
y = a sin(kx – ωt) – a sin(kx + ωt)
y = (2asinkx)cosωt
2a sin kx = Amplitude of resultant wave.
It depend on 'kx'. If x = 0, λ/2, 2λ/2, 3λ/2 ...... etc, the amplitude = zero
These positions are known as "Nodes"
If x = λ/4, 3λ/4, 5λ/4 ...... etc, the amplitude = maximum (2a). These positions are called "Antinodes"
Formation of stationary waves : A stretched string can be vibrate in different frequencies and form stationary wave. This mode of vibrations are known as Harmonics.
If it vibrates in one segment, which known as 'Fundamental Harmonic'. The Higher Harmonics are called the overtones.
It vibrates in two segments then the second Harmonic is called first overtone. Similarly the patterns of vibrations are as shown in figure.
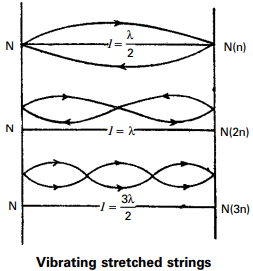
If the string vibrates in 'P' segments and 'l' is its length then length of each segment = l/p
Which is equal to λ/2
∴ l/p = λ/2 ⇒ λ = 2l/p
Harmonic frequency v = v/λ = vp/2l
v = vp/2l ......(1)
If 'T' is tension (stretching force) in the string and 'µ' is linear density then velocity of transverse wave (v) in the string is
From the Eqs (1) and (2)
v = √(T/µ) ......(2)
Harmonic frequency ν = p/2l√(T/µ)
If p = 1 then it is called fundamental frequency (or) first harmonic frequency
∴ Fundamental Frequency ν = 1/2l√(T/µ) ......(3)
If p = 2 then it is first overtone (or) second harmonic frequency.
v1 = 2/2l√(T/µ) = 2v .....(4)
Similarly if p = 3 then second overtone (or) third harmonic frequency
v2 = 3/2l√(T/µ) = 3v .....(5)
from the Eqs (3), (4) and (5)
The ratio of the frequencies of harmonics are ν : ν1 : ν2 = ν : 2ν : 3ν = 1 : 2 : 3
∴ The frequencies of the overtones in a given vibrating length, are integral multiples of the fundamental in the same length.
Laws of Transverse Waves along Stretched String :
Fundamental frequency of the vibrating string ν = 1/2l√(T/µ)
First Law : When the tension (T) and linear density (µ) are constant, the fundamental frequency (ν) of a vibrating string is inversely proportional to its length.
∴ ν ∝ 1/l ⇒ νl = constant, when 'T' and 'µ' are constant.
Second Law : When the length (l) and its, linear density (m) are constant the fundamental frequency of a vibrating string is directly proportional to the square root of the stretching force (T).
∴ ν ∝ √T ⇒ ν/√T = constant, when 'l' and 'm' are constant.
Third Law : When the length (l) and the tension (T) are constant, the fundamental frequency of a vibrating string is inversely proportional to the square root of the linear density (m).
ν ∝ 1/√µ ⇒ ν√µ = constant, when 'l' and 'T' are constant.
Problem :
