Question

A series LCR circuit is connected to an ac source having voltage v = v_msinωt. Derive the expression for the instantaneous current J and its phase relationship to the applied voltage. Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.

Answer 1

Suppose resistance R, inductance L and capacitance C are connected in series and an alternating source of voltage V =V₀sinωt is applied across it. (fig. a) On account of being in series, the current (i ) flowing through all of them is the same.

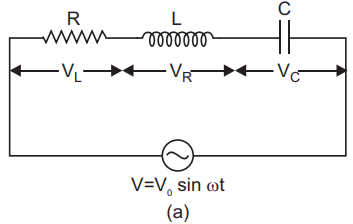
Suppose the voltage across resistance R is V_R, voltage across inductance L is V_L  and voltage across capacitance C is V_C. The voltage V_R  and current i are in the same phase, the voltage V_L  will lead the current by angle 90° while the voltage V_C will lag behind the current by angle 90° (fig. b). Clearly V_C  and V_L are in opposite directions, therefore their resultant potential difference =V_C -V_L (if V_C >V_C ). 

Thus V_R  and (V_C - V_L) are mutually perpendicular and the phase difference between them is 90°. As applied voltage across the circuit is V, the resultant of V_R  and (V_C - V_L) will also be V. From fig.

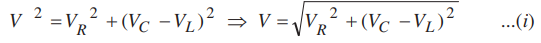
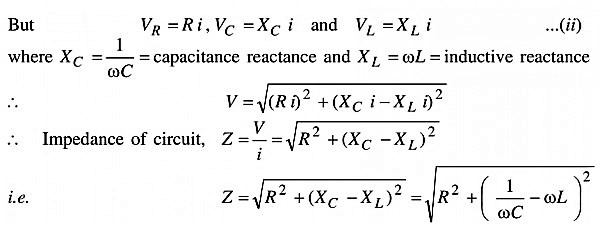
Instantaneous current 

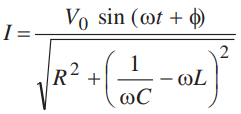
Condition for resonance to occur in series LCR ac circuit: 

For resonance the current produced in the circuit and emf applied must always be in the same phase. 

Phase difference (ϕ) in series LCR circuit is given by

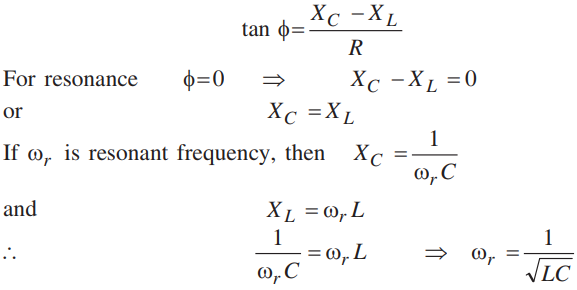
Power factor is the cosine of phase angle ϕ, i.e., cosϕ = R/Z.

For maximum power cosϕ =1 or Z = R 

i.e., circuit is purely resistive. 

For minimum power cosϕ = 0 or R = 0 

i.e., circuit should be free from ohmic resistance.