Question

A metallic right circular cone 20 cm high and whose vertical angle is 60º is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \(\frac{1}{16}\) cm,  find the length of the wire.

(a) 6497.44 m 

(b) 4967.44 m 

(c) 7964.44 m 

(d) 6794.44 m

Answer 1

Answer: (c) =7964.44 m

Given 

\(<\)BAC = 60º ⇒ \(<\)DAC = 30º. 

AD = 20 cm 

⇒ AE = ED = 10 cm.

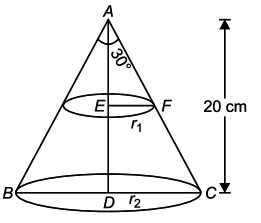
In △AEF, tan 30º = \(\frac{EF}{AE}\)  

⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{r_1}{10}\) 

⇒ r₁ = \(\frac{10}{\sqrt{3}}\) cm

In △ADC, tan 30º = \(\frac{DC}{AD}\) 

⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{r_2}{10}\) 

⇒ r₂ = \(\frac{20}{\sqrt{3}}\) cm

∴ Volume of the frustum cut by the plane 

= \(\frac{\pi h}{3}(r_1^2+r_2^2+r_1r_2)\) 

= \(\frac{\pi \times 10}{3}\big(\frac{100}{3}+\frac{400}{3}+\frac{200}{3}\big) = \frac{7000\pi}{9}\) cm³  

Let the length of the wire be h cm.

Given, radius of wire = \(\frac{1}{32}\) cm.

∴ Volume of wire (cylinder) =π ×\(\big(\frac{1}{32}\big)^2 \times h\) 

So, \(\frac{7000\pi}{9} =\frac{\pi h}{32 \times 32} \)  

⇒ h = \(\frac{7000\times 32\times 32}{9}\) cm

= \(\frac{7000\times 32\times 32}{9 \times 100}\) m 

=7964.44 m