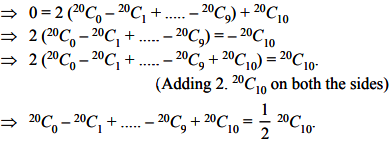Question

The sum of the series ²⁰C₀ – ²⁰C₁ + ²⁰C₂ – ²⁰C₃ + ...... + ²⁰C₁₀ is

(a) ²⁰C₁₀ 

(b)  \(\frac{1}{2}\)²⁰C₁₀ 

(c) 0 

(d) ²⁰C₁₅

Answer 1

Answer : (b)  \(\frac{1}{2}\)²⁰C₁₀

(1 + x) ²⁰ = ²⁰C₀ + ²⁰C₁ x + ²⁰C₂ x² + ²⁰C₃ x³ + ..... + ²⁰C₁₉ x¹⁹ + ²⁰C₂₀ x²⁰

On putting x = – 1, we get

0 = ²⁰C₀ – ²⁰C₁ + ²⁰C₂ – ²⁰C₃ + ..... – ²⁰C₁₉ + ²⁰C₂₀

⇒ 0 = ²⁰C₀ – ²⁰C₁ + ..... – ²⁰C₉ + ²⁰C₁₀ – ²⁰C₉ + ²⁰C₈ .... + ²⁰C₀ 

(∵ ⁿC_r = ⁿC_n–r )