Question

NCERT Solutions Class 11 Maths Chapter 3 Trigonometric Functions is the best study material available online for the preparation for competitive exams like JEE Mains, JEE Advance, Olympiad, or NTSE. One must refer to our NCERT Solutions to learn the basic concepts of mathematics.

In this NCERT Solutions Class 11, we have covered all the important topics in detail.

• Trigonometric Functions – trigonometric functions are also called circular functions. It can also be defined as the function of the angle of a triangle. The trigonometric function is the relationship between the angle of a triangle and the side of a triangle. Some basic trigonometric functions are sine, cosine, tangent, cotangent, secant, and cosecant.
  • Sine function – sine function of any angle is the relation between the opposite side to the hypotenuse. Sin a =  opposite/hypotenuse
  • Cos function - cos function of any angle is the relation adjacent opposite side of the hypotenuse. Cos a = adjacent/hypotenuse
  • Tan function - the tan function of any angle is the relation adjacent opposite side to the opposite side. Tan a = adjacent/opposite
  • Sec a = hypotenuse/adjacent
  • Cosec a = hypotenuse/opposite
  • Cot a = adjacent/opposite

• Positive angles – positive angles are angles measured in an anti-clockwise fashion.
• Negative angles – negative angles are angles measured in a clockwise fashion.

• Measuring angles in radians and degrees and conversion of one into other

• Definition of trigonometric functions with the help of unit circle

• Truth of the sin²x + cos²x = 1, for all x

• Signs of trigonometric functions – in quadrant I, all the signs are positive. In quadrant II, sin θ and csc θ are positive. In quadrant III, tan θ and cot θ are positive. In quadrant IV, cos θ and sec θ are positive.

• Domain and range of trigonometric functions

• Graphs of Trigonometric Functions

• General solution of trigonometric equations of the type sin y = sin a cos y = cos a, and tan y = tan a

In this NCERT Solutions Class 11 Maths, we have provided detailed explanations for better learning and doing homework, and completing assignments.

Answer 1

NCERT Solutions Class 11 Maths Chapter 3 Trigonometric Functions

1. Find the radian measures corresponding to the following degree measures: 

(i) 25°

(ii) – 47° 30'

(iii) 240°

(iv) 520°

Answer:

(i) 25°

We know that 180° = π radian

 

(ii)–47° 30'

–47° 30  \(-47\frac12\)

= \(\frac{-95}2\)

Since 180° = π radian

(iii) 240°

We know that 180° = π radian

(iv) 520°

We know that 180° = π radian

2. Find the degree measures corresponding to the following radian measures (Use π = 22/7).

(i) 11/16

(ii) – 4 

(iii) 5π/3

(iv) 7π/6

Answer:

(i) 11/16

We know that π radian = 180°

(ii) – 4

We know that π radian = 180°

(iii) 5π/3

We know that π radian = 180°

(iv) 7π/6

We know that π radian = 180°

3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

Answer:

Number of revolutions made by the wheel in 1 minute = 360 

∴ Number of revolutions made by the wheel in 1 second = 360/60 = 6

In one complete revolution, the wheel turns an angle of 2π radian. 

Hence, in 6 complete revolutions, it will turn an angle of 6 × 2π radian, i.e., 12 π radian 

Thus, in one second, the wheel turns an angle of 12π radian.

4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm. (Use π = 22/7)

Answer:

We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then

θ = 1/r

Therefore, forr = 100 cm, l = 22 cm, we have

Thus, the required angle is 12°36′.

5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

Answer:

Diameter of the circle = 40 cm 

∴ Radius (r) of the circle = 40/2 cm = 20 cm

Let AB be a chord (length = 20 cm) of the circle.

In ∆OAB, OA = OB = Radius of circle = 20 cm 

Also, AB = 20 cm 

Thus, ∆OAB is an equilateral triangle.

∴ θ = 60° = π/3 radian

We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ

Thus, the length of the minor arc of the chord is \(\frac{20\pi}3\) cm

6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.

Answer:

Let the radii of the two circles be r₁ and r₂. Let an arc of length l subtend an angle of 60° at the centre of the circle of radius r₁, while let an arc of length l subtend an angle of 75° at the centre of the circle of radius r₂.

Now, 60°= \(\frac{\pi}{3}\) radian and 75° = \(\frac{5\pi}{12}\) radian

We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ

Thus, the ratio of the radii is 5:4.

7. Find the angle in radian though which a pendulum swings if its length is 75 cm and the tip describes an arc of length 

(i) 10 cm 

(ii) 15 cm 

(iii) 21 cm

Answer:

We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = l/r

It is given that r = 75 cm

(i) Here, l = 10 cm

(ii) Here, l = 15 cm

(iii) Here, l = 21 cm

8. Find the values of other five trigonometric functions if cos x = \(-\frac12\), x lies in third quadrant.

Answer:

Since x lies in the 3^rd quadrant, the value of sin x will be negative.

9. Find the values of other five trigonometric functions if sin x = 3/5, x lies in second quadrant.

Answer:

Since x lies in the 2^nd quadrant, the value of cos x will be negative

Answer 2

10. Find the values of other five trigonometric functions if cot x = 3/4, x lies in third quadrant.

Answer:

Since x lies in the 3^rd quadrant, the value of sec x will be negative.

11. Find the values of other five trigonometric functions if sec x = 13/5 , x lies in fourth quadrant.

Answer:

Since x lies in the 4^th quadrant, the value of sin x will be negative.

12. Find the values of other five trigonometric functions if tan x = \(-\frac5{12}\), x lies in second quadrant.

Answer:

Since x lies in the 2^nd quadrant, the value of sec x will be negative.

13. Find the value of the trigonometric function sin 765°

Answer:

It is known that the values of sin x repeat after an interval of 2π or 360°.

14. Find the value of the trigonometric function cosec (–1410°)

Answer:

It is known that the values of cosec x repeat after an interval of 2π or 360°.

15. Find the value of the trigonometric function \(tan\frac{19x}{3}\)

Answer:

It is known that the values of tan x repeat after an interval of π or 180°.

16. Find the value of the trigonometric function \(sin(-\frac{11\pi}{3})\)

Answer:

It is known that the values of sin x repeat after an interval of 2π or 360°.

17. Find the value of the trigonometric function \(cot(-\frac{15\pi}{4})\)

Answer:

It is known that the values of cot x repeat after an interval of π or 180°.

18. \(sin^2\frac{\pi}{6}+cos^2\frac{\pi}3-tan^2\frac{\pi}{4}=-\frac12\)

Answer:

19. Prove that \(2sin^2\frac{\pi}6+cosec^2\frac{7\pi}{6}cos^2\frac{\pi}{3}=\frac32\)

Answer:

20. Prove that \(cot^2\frac{\pi}{6}+cosec\frac{5\pi}{6}+3tan^2\frac{\pi}{6}=6\)

Answer:

21. Prove that \(2sin^2\frac{3\pi}{4}+2cos^2\frac{\pi}{4}+2sec^2\frac{\pi}{3}= 10\)

Answer:

L.H.S = \(2sin^2\frac{3\pi}{4}+2cos^2\frac{\pi}{4}+2sec^2\frac{\pi}{3}\) 

22. Find the value of: 

(i) sin 75° 

(ii) tan 15°

Answer:

(i) sin 75° = sin (45° + 30°) 

= sin 45° cos 30° + cos 45° sin 30° 

[sin (x + y) = sin x cos y + cos x sin y]

(ii) tan 15° = tan (45° – 30°)

 23. Prove that:

Answer:

24. Prove that:

Answer:

It is known that

L.H.S. =

25. Prove that

Answer:

 26.

 

Answer:

27. Prove that sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x

Answer:

L.H.S. = sin (n + 1)x sin(n + 2)x + cos (n + 1)x cos(n + 2)x

28. Prove that \(cos(\frac{3\pi}{4}+x)-cos(\frac{3\pi}{4}-x)=-\sqrt{2}sin\, x\)

Answer:

It is known that

cos A - cos B = -2 sin (\(\frac{A+B}{2}\)).sin(\(\frac{A-B}{2}\))

∴ L.H.S. = \(cos(\frac{3\pi}{4}+x)-cos(\frac{3\pi}{4}-x)\)  

29. Prove that sin² 6x – sin² 4x = sin 2x sin 10x

Answer:

It is known that

∴ L.H.S. = sin²6x – sin²4x 

= (sin 6x + sin 4x) (sin 6x – sin 4x)

= (2 sin 5x cos x) (2 cos 5x sin x) 

= (2 sin 5x cos 5x) (2 sin x cos x) 

= sin 10x sin 2x 

= R.H.S.

Answer 3

30. Prove that cos² 2x – cos² 6x = sin 4x sin 8x

Answer:

It is known that

∴ L.H.S. = cos² 2x – cos² 6x 

= (cos 2x + cos 6x) (cos 2x – 6x)

= [2 cos 4x cos 2x] [–2 sin 4x (–sin 2x)]

= (2 sin 4x cos 4x) (2 sin 2x cos 2x) 

= sin 8x sin 4x = R.H.S.

31. Prove that sin 2x + 2sin 4x + sin 6x = 4cos² x sin 4x

Answer:

L.H.S. = sin 2x + 2 sin 4x + sin 6x 

= [sin 2x + sin 6x] + 2 sin 4x

= 2 sin 4x cos (– 2x) + 2 sin 4x 

= 2 sin 4x cos 2x + 2 sin 4x 

= 2 sin 4x (cos 2x + 1) 

= 2 sin 4x (2 cos² x – 1 + 1) 

= 2 sin 4x (2 cos² x) 

= 4cos² x sin 

4x = R.H.S.

32. Prove that cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

Answer:

L.H.S = cot 4x (sin 5x + sin 3x)

= 2 cos 4x cos x 

R.H.S. = cot x (sin 5x – sin 3x)

= 2 cos 4x. cos x 

L.H.S. = R.H.S.

33. Prove that \(\cfrac{cos9x - cos5x}{sin17x-sin3x}=-\cfrac{sin2x}{cos10x}\)

Answer:

It is known that

∴  L.H.S = \(\cfrac{cos9x - cos5x}{sin17x-sin3x}\) 

34. Prove that :

\(\cfrac{sin\,5x + sin\,3x}{cos\,5x + cos\,3x} = tan \,4x\)

Answer:

It is known that

∴L.H.S. = \(\cfrac{sin\,5x + sin\,3x}{cos\,5x + cos\,3x} \)

35. Prove that \(\cfrac{sin\,x-sin\,y}{cos\,x+cos\,y}=tan\frac{x-y}{2}\) 

Answer:

It is known that

∴ L.H.S. = \(\cfrac{sin\,x-sin\,y}{cos\,x+cos\,y}\) 

36. Prove that \(\cfrac{sin\,x+sin\,3x}{cos\,x+cos\,3x}=tan2x \) 

Answer:

It is known that

∴ L.H.S. = \(\cfrac{sin\,x+sin\,3x}{cos\,x+cos\,3x}\) 

37. Prove that \(\cfrac{sin\,x-sin\,3x}{sin^2x- cos^2x}= 2sin\,x\)

Answer:

It is known that

38. Prove that

 \(\cfrac{cos\,4x+cos\,3x+cos\,2x}{sin\,4x+sin\,3x+sin\,2x}= cot\,3x\)

Answer:

L.H.S. = \(\cfrac{cos\,4x+cos\,3x+cos\,2x}{sin\,4x+sin\,3x+sin\,2x}\)

39. Prove that cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1

Answer:

L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x 

= cot x cot 2x – cot 3x (cot 2x + cot x) 

= cot x cot 2x – cot (2x + x) (cot 2x + cot x)

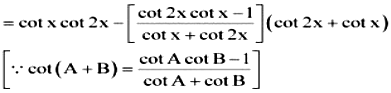
= cot x cot 2x – (cot 2x cot x – 1) = 1 = R.H.S.

40. Prove that  \(tan\,4x=\cfrac{4\,tan\,x(1-tan^2x)}{1-6\,tan^2x+tan^4x}\)

Answer:

It is known that. 

\(tan\,2A = \frac{2\,tan\,A}{1-tan^2\,A}\)

∴ L.H.S. = tan 4x = tan 2(2x)

41. Prove that: cos 4x = 1 – 8sin²x cos²x

Answer:

L.H.S. = cos 4x 

= cos 2(2x) 

= 1 – 2 sin² 2x [cos 2A = 1 – 2 sin² A] 

= 1 – 2(2 sin x cos x)² [sin²A = 2sin A cosA] 

= 1 – 8 sin²x 

cos²x = R.H.S

42. Prove that: cos 6x = 32 cos⁶ x – 48 cos⁴ x + 18 cos² x – 1

Answer:

L.H.S. = cos 6x

= cos 3(2x)

= 4 cos³ 2x – 3 cos 2x [cos 3A = 4 cos³ A – 3 cos A]

= 4 [(2 cos² x – 1)³ – 3 (2 cos² x – 1) [cos 2x = 2 cos² x – 1]

= 4 [(2 cos² x)³ – (1)³ – 3 (2 cos² x)² + 3 (2 cos² x)] – 6cos² x + 3

= 4 [8cos⁶x – 1 – 12 cos⁴x + 6 cos²x] – 6 cos²x + 3

= 32 cos⁶x – 4 – 48 cos⁴x + 24 cos² x – 6 cos²x + 3

= 32 cos⁶x – 48 cos⁴x + 18

cos²x – 1 = R.H.S.

43. Find the principal and general solutions of the equation tan x = \(\sqrt{3}\) 

Answer:

tan x = \(\sqrt{3}\) 

It is known that tan \(\frac{\pi}{3}=\sqrt{3}\) and tan (\(\frac{4\pi}{3}\)) = tan(\(\pi+\frac{\pi}{3}\)) = \(tan\frac{\pi}{3}= \sqrt{3}\) 

Therefore, the principal solutions are x = \(\frac{\pi}{3}\) and \(\frac{4\pi}{3}\).

Now, tan x = tan\(\frac{\pi}{3}\) 

⇒ x = nπ + \(\frac{\pi}{3}\) , where n \(\in\) Z

Answer 4

44. Find the principal and general solutions of the equation sec x = 2

Answer:

sec x = 2

It is known that sec\(\frac{\pi}{3}\) = 2 and sec \(\frac{5\pi}{3}\) = sec (2π - \(\frac{\pi}{3}\)) = sec\(\frac{\pi}{3}\) = 2

Therefore, the principal solutions are x = \(\frac{\pi}{3}\) and \(\frac{5\pi}{3}\) .

Therefore, the general solution is  \(x=2n\pi\pm\frac{\pi}{3}\) , where n \(\in\) Z

45. Find the principal and general solutions of the equation cot x = - √3

Answer:

cot x = - √3

Therefore, the principal solutions are x = \(\frac{5\pi}{6}\) and \(\frac{11\pi}{6}\) .

Therefore, the general solution is x = nπ + \(\frac{5\pi}{6}\) , where  n \(\in\) Z

46. Find the general solution of cosec x = –2

Answer:

cosec x = –2

It is known that

cosec\(\frac{\pi}{6}\) = 2

Therefore, the principal solutions are x = \(\frac{7\pi}{6}\) and \(\frac{11\pi}{6}\) .

Therefore, the general solution is x = nπ + (-1)ⁿ \(\frac{7\pi}{6}\) , where  n \(\in\) Z

47. Find the general solution of the equation cos 4x = cos 2x

Answer:

cos 4x = cos 2x

⇒ cos 4x - cos 2x = 0

48. Find the general solution of the equation cos 3x + cos x - cos 2x = 0

Answer:

cos 3x + cos x - cos 2x = 0

49. Find the general solution of the equation sin 2x + cos x = 0

Answer:

sin 2x + cos x = 0

Therefore, the general solution is (2n +1) \(\frac{\pi}{2}\) or nπ + (-1)n \(\frac{7\pi}{6}\), n \(\in\) Z

50.Find the general solution of the equation sec² 2x = 1 - tan 2x

Answer:

sec² 2x = 1 - tan 2x

Therefore, the general solution is \(\frac{n\pi}{2}\) or \(\frac{n\pi}{2}+\frac{3\pi}{8}\), n \(\in\) Z

51. Find the general solution of the equation sin x + sin 3x + sin 5x = 0

Answer:

sin x + sin 3x + sin 5x = 0

(sin x + sin 5x) + sin 3x = 0

Therefore, the general solution is \(\frac{n\pi}{2}\) or nπ \(\pm\) \(\frac{\pi}{3}\), n \(\in\) Z

52. Prove that:

\(2\,cos\frac{\pi}{13}\,cos\frac{9\pi}{13}+cos\frac{3\pi}{13}+cos\frac{5\pi}{13}= 0\)

Answer:

L.H.S

= 0 = R.H.S

53. Prove that: (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0

Answer:

L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x

54. Prove that: 

(cos x + cos y)² + (sin x - sin y)² = 4 cos² \(\frac{x+y}2\) 

Answer:

L.H.S. = (cos x + cos y)² + (sin x - sin y)²

= 4 cos² (\(\frac{x+y}2\)) = R.H.S.

55. Prove that:

(cos x - cos y)² + (sin x - sin y)² = 4 sin² \(\frac{x-y}2\) 

Answer:

L.H.S. = (cos x - cos y)² + (sin x - sin y)²

= 4 sin² (\(\frac{x-y}2\)) = R.H.S

56. Prove that: 

sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x  sin 4x

Answer:

It is known that 

sin A + sin B = 2 sin (\(\frac{A+B}{2}\)).cos(\(\frac{A-B}{2}\))

57. Prove that:

Answer:

It is known that

sin A + sin B = 2 sin (\(\frac{A+B}{2}\)).cos(\(\frac{A-B}{2}\)) , cos A + cos B = 2 cos (\(\frac{A+B}{2}\)).cos(\(\frac{A-B}{2}\))

L.H.S. =

= tan 6x 

= R.H.S.

Answer 5

58. Prove that:

sin 3x + sin 2x - sin x = 4 sin x cos\(\frac x2\) cos \(\frac {3x}2\)

Answer:

L.H.S. = sin 3x + sin 2x - sin x

= sin 3x + (sin 2x - sin x)

59. Find sin x/2, cos x/2 and tan x/2 , if tan x = \(-\frac43\), x in quadrant II

Answer:

Here, x is in quadrant II.

Therefore, sin x/2, cos x/2 and tan x/2 are lies in first quadrant.

It is given that tan x = \(-\frac43\).

As x is in quadrant II, cos x is negative.

Thus, the respective values of 

.

60. Find, sin x/2, cos x/2 and tan x/2 for cos x = \(-\frac13\), x in quadrant III

Answer:

Here, x is in quadrant III.

Therefore, cos x/2 and tan x/2 are negative, where sin x/2 as is positive.

It is given that cos x = - 1/3

Now

cos x = 2cos² \(\frac x2-1\) 

Thus, the respective values of 

 .

61. Find sin x/2, cos x/2 and tan x/2 for sin x = 1/4, x in quadrant II

Answer:

Here, x is in quadrant II.

Therefore, sin x/2, cos x/2 and tan x/2 are all positive.

Thus, the respective values of sin x/2, cos x/2 and tan x/2 are \(\frac{\sqrt{8+2\sqrt{15}}}{4}\), \(\frac{\sqrt{8-2\sqrt{15}}}{4}\) , and 4 + \(\sqrt{15}\)