If the shortest distance between the lines x-1/2 = y-2/3 = z-3/4 and x/1 = y/α = z-5/1 is 5/√6, then the sum of all possible values of α is

Question

If the shortest distance between the lines \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) and \(\frac{x}{1}=\frac{y}{\alpha}=\frac{z-5}{1}\) is \(\frac{5}{\sqrt{6}},\) then the sum of all possible values of \(\alpha\) is

(1) \(\frac{3}{2}\)

(2) \(-\frac{3}{2}\)

(3) 3

(4) -3 

Answer 1

Correct option is: (4) -3  

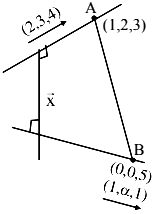
\(L_{1}: \frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}-2}{3}=\frac{\mathrm{z}-3}{4}\)

\(\mathrm{L}_{1}: \frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{\alpha}=\frac{\mathrm{z}-5}{1}\)

\(\overrightarrow{\mathrm{x}}=\left|\begin{array}{lll}\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{k} \\ 2 & 3 & 4 \\ 1 & \alpha & 1\end{array}\right|=\hat{\mathrm{i}}(3-4 \alpha)-\hat{\mathrm{j}}(-2)+\hat{\mathrm{k}}(2 \alpha-3)\)  

S.D. \(=\left|\frac{\overrightarrow{\mathrm{BA}} \cdot \vec{n}}{|\overrightarrow{\mathrm{n}}|}\right|=\left|\frac{(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-2 \hat{\mathrm{k}}) \cdot \overrightarrow{\mathrm{n}}}{|\overrightarrow{\mathrm{n}}|}\right|\)

\(\Rightarrow 6(13-8 \alpha)^{2}=25\left((4 \alpha-3)^{2}+(2 \alpha-3)^{2}+16\right)\)

\(6\left(64 a^{2}-280 \alpha+169\right)=25\left(20 \alpha^{2}-36 \alpha+34\right)\)

\(\Rightarrow 116 \alpha^{2}+348 \alpha-164=0\)

\(\alpha_{1}+\alpha_{2}=\frac{-348}{116}=-3\)