Let the set of all values of p ∈ R, for which both the roots of the equation x^2 – (p + 2)x + (2p + 9) = 0 are negative real numbers,

Question

Let the set of all values of \(p \in \mathbb{R},\) for which both the roots of the equation \(x^{2}-(p+2) x+(2 p+9)=0\) are negative real numbers, be the interval \((\alpha, \beta].\) Then \(\beta-2 \alpha\) is equal to

(1) 0

(2) 9

(3) 5

(4) 20 

Answer 1

Correct option is: (3) 5 

Using location of roots : 

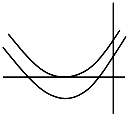
(i) \(\mathrm{D} \geq 0\)

(ii) \(\frac{-\mathrm{b}}{2 \mathrm{a}}<0\)

(iii) \(a. \mathrm{f}(0)>0\)

\((p+2)^{2}-4(2 p+9) \geq 0\)

\((p+4)(p-8) \geq 0 \quad \mathrm{p}+2<0 \quad 2 \mathrm{p}+9>0\)

Intersection \(\mathrm{p} \in\left(-\frac{9}{2},-4\right]\)

\(\therefore\ \beta-2 \alpha=-4+9=5\)